题目内容
已知点
，设
（O为坐标 原点）
（1）求y关于x的函数关系式y=f（x），并求f（x）的最小正周期；
（2）若
上的最小值．
解：（1）依题意得：
，
∴
a=
，
∴f（x）的最小正周期为π．
（2）若
，∴
，
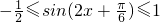故 ymax =2+1+a=4，∴a=1，ymin =-1+1+a=a=1．
分析：（1）利用两个向量的数量积公式化简函数f（x）的解析式为，求出周期．
（2）根据x的范围，可得角2x+
的范围，得到sin（2x+ ）的值域，从而求得最值．
点评：本题考查两个向量的数量积公式，两角和正弦公式，以及正弦函数的周期性、值域，化简函数f（x）的解析式，是解题的突破口．
，∴
a=，∴f（x）的最小正周期为π．
（2）若
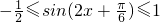，∴，故 ymax =2+1+a=4，∴a=1，ymin =-1+1+a=a=1．
分析：（1）利用两个向量的数量积公式化简函数f（x）的解析式为
，求出周期．（2）根据x的范围，可得角2x+
的范围，得到sin（2x+ ）的值域，从而求得最值．点评：本题考查两个向量的数量积公式，两角和正弦公式，以及正弦函数的周期性、值域，化简函数f（x）的解析式，是解题的突破口．
练习册系列答案
阅读快车系列答案
相关题目
，设
（O为坐标 原点）
上的最小值．