题目内容
已知函数 (a>0且a≠1),现给出下列命题:
(a>0且a≠1),现给出下列命题:
①当其图象是一条连续不断的曲线时,则a= ;
;
②当其图象是一条连续不断的曲线时,能找到一个非零实数a使f(x)在(-∞,+∞)上是增函数;
③当 时,不等式f(1+a)•f(1-a)<0恒成立;
时,不等式f(1+a)•f(1-a)<0恒成立;
④函数y=f(|x+1|)是偶函数.
其中正确命题的序号是________.(填上所有你认为正确的命题的序号)
①③
分析:①要满足条件,则需要(3a-1)×1+5a=loga1,解得即可;
②由①可得a的值,看是否满足增函数即可;
③由条件分别判断f(1+a)与f(1-a)的符号即可;
④根据偶函数的定义判断即可.
解答:①当其图象是一条连续不断的曲线时,则a满足:a<0,a≠1,且(3a-1)×1+5a=loga1=0,解得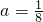 ,故①正确;
,故①正确;
②当其图象是一条连续不断的曲线时,假设能找到一个非零实数a使f(x)在(-∞,+∞)上是增函数,则a必须满足 ,解得a不存在,故②不正确;
,解得a不存在,故②不正确;
或由①可知:当其图象是一条连续不断的曲线时,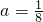 ,而此时
,而此时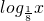 是减函数,故不符合题意,应舍去,即满足题意的a不存在;
是减函数,故不符合题意,应舍去,即满足题意的a不存在;
③当 时,1+a>1,1-a<1,∴f(1+a)=loga(1+a)<0,
时,1+a>1,1-a<1,∴f(1+a)=loga(1+a)<0,
f(1-a)=(3a-1)(1-a)+5a=-3a2+9a-1= ,当
,当 时,此函数单调递增,而
时,此函数单调递增,而 =
= >0,
>0,
∴当 时,不等式f(1+a)•f(1-a)<0恒成立,即③正确;
时,不等式f(1+a)•f(1-a)<0恒成立,即③正确;
④y=f(|x+1|= ,其图象关于y轴不对称,故不是偶函数,即④不正确.
,其图象关于y轴不对称,故不是偶函数,即④不正确.
综上可知:只有①③正确.
故答案为①③.
点评:正确理解函数的单调性和奇偶性是解题的关键.
分析:①要满足条件,则需要(3a-1)×1+5a=loga1,解得即可;
②由①可得a的值,看是否满足增函数即可;
③由条件分别判断f(1+a)与f(1-a)的符号即可;
④根据偶函数的定义判断即可.
解答:①当其图象是一条连续不断的曲线时,则a满足:a<0,a≠1,且(3a-1)×1+5a=loga1=0,解得
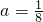 ,故①正确;
,故①正确;②当其图象是一条连续不断的曲线时,假设能找到一个非零实数a使f(x)在(-∞,+∞)上是增函数,则a必须满足
 ,解得a不存在,故②不正确;
,解得a不存在,故②不正确;或由①可知:当其图象是一条连续不断的曲线时,
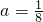 ,而此时
,而此时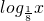 是减函数,故不符合题意,应舍去,即满足题意的a不存在;
是减函数,故不符合题意,应舍去,即满足题意的a不存在;③当
 时,1+a>1,1-a<1,∴f(1+a)=loga(1+a)<0,
时,1+a>1,1-a<1,∴f(1+a)=loga(1+a)<0,f(1-a)=(3a-1)(1-a)+5a=-3a2+9a-1=
 ,当
,当 时,此函数单调递增,而
时,此函数单调递增,而 =
= >0,
>0,∴当
 时,不等式f(1+a)•f(1-a)<0恒成立,即③正确;
时,不等式f(1+a)•f(1-a)<0恒成立,即③正确;④y=f(|x+1|=
 ,其图象关于y轴不对称,故不是偶函数,即④不正确.
,其图象关于y轴不对称,故不是偶函数,即④不正确.综上可知:只有①③正确.
故答案为①③.
点评:正确理解函数的单调性和奇偶性是解题的关键.

练习册系列答案
相关题目
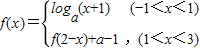 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )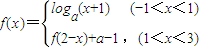 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( ) (a>0且a为常数).
(a>0且a为常数). 对x∈[-
对x∈[- ,+∞)恒成立,求a的取值范围.
,+∞)恒成立,求a的取值范围. 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. =loga
=loga (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数 ,(
,(