题目内容
已知数列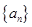 的前n项和是
的前n项和是 ,且
,且 则
则 .
.
-2n+4
解析试题分析:因为,
所以,n=1时, =2,
=2,
当 时,由
时,由

 两式两边分别相减得,
两式两边分别相减得, -2n+4,验证知,n=1时,
-2n+4,验证知,n=1时, =2,适合上式,故
=2,适合上式,故 -2n+4。
-2n+4。
考点:本题主要考查等差数列的通项公式、求和公式。
点评:简单题,涉及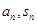 ,往往通过研究
,往往通过研究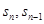 的差,发现结论。
的差,发现结论。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
题目内容
已知数列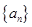 的前n项和是
的前n项和是 ,且
,且 则
则 .
.
-2n+4
解析试题分析:因为,
所以,n=1时, =2,
=2,
当 时,由
时,由

 两式两边分别相减得,
两式两边分别相减得, -2n+4,验证知,n=1时,
-2n+4,验证知,n=1时, =2,适合上式,故
=2,适合上式,故 -2n+4。
-2n+4。
考点:本题主要考查等差数列的通项公式、求和公式。
点评:简单题,涉及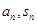 ,往往通过研究
,往往通过研究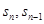 的差,发现结论。
的差,发现结论。

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案