题目内容
已知函数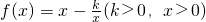
，则f（x2+1）与f（x）的大小关系为________．
f（x2+1）＞f（x）
分析：确定函数在（0，+∞）上单调增，利用函数的单调性，即可得到结论．
解答：由题意，求导函数，可得f′（x）=1+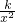
＞0
∴函数在（0，+∞）上单调增
∵x2+1＞x＞0
∴f（x2+1）＞f（x）
故答案为：f（x2+1）＞f（x）
点评：本题考查函数的单调性，解题的关键是确定函数的单调性，属于基础题．
分析：确定函数在（0，+∞）上单调增，利用函数的单调性，即可得到结论．
解答：由题意，求导函数，可得f′（x）=1+
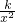＞0∴函数在（0，+∞）上单调增
∵x2+1＞x＞0
∴f（x2+1）＞f（x）
故答案为：f（x2+1）＞f（x）
点评：本题考查函数的单调性，解题的关键是确定函数的单调性，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
，则|f（a）|＜2（其中f（a）表示函数y=f（x）在x=a时的函数值）；
，则|f（a）|＜2（其中f（a）表示函数y=f（x）在x=a时的函数值）；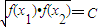
，则称常数C是函数f（x）在D上的“翔宇一品数”．若已知函数
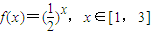，则f（x）在[1，3]上的“翔宇一品数”是 ．
，则f（x2+1）与f（x）的大小关系为（ ）