Question

(08年四川卷文)（本小题满分12分）

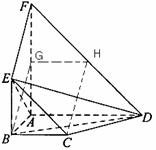
  如图，平面平面，四边形与都是直角梯形，

，，分别为的中点

（Ⅰ）证明：四边形是平行四边形；

（Ⅱ）四点是否共面？为什么？

（Ⅲ）设，证明：平面平面；

Answer 1

解法一：

（Ⅰ）由题意知，

所以

又，故

所以四边形是平行四边形。

（Ⅱ）四点共面。理由如下：

由，是的中点知，，所以

由（Ⅰ）知，所以，故共面。又点在直线上

所以四点共面。

（Ⅲ）连结，由，及知是正方形

故。由题设知两两垂直，故平面，

因此是在平面内的射影，根据三垂线定理，

又，所以平面

由（Ⅰ）知，所以平面。

由（Ⅱ）知平面，故平面，得平面平面

 

解法二：

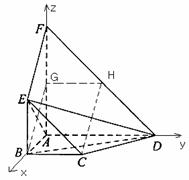
由平面平面，，得平面，以为坐标原点，

射线为轴正半轴，建立如图所示的直角坐标系

（Ⅰ）设，则由题设得

　　

所以

于是

又点不在直线上

所以四边形是平行四边形。

（Ⅱ）四点共面。理由如下：

由题设知，所以

又，故四点共面。

（Ⅲ）由得，所以

又，因此

即

又，所以平面

故由平面，得平面平面