题目内容
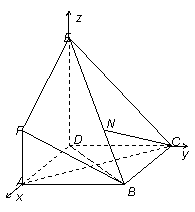
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2,AF=1.
(1)证明: BE⊥AC;
(2)在棱BE上是否存在一点N,,使得直线CN与平面ADE成30°角,若存在,求出BN的长度:若不存在,说明理由。

解:(Ⅰ)法一:连结BD,∵ABCD是正方形,
 ∴BD⊥AC. - ∵AF⊥平面ABCD,DE∥AF,
∴BD⊥AC. - ∵AF⊥平面ABCD,DE∥AF,
∴DE⊥平面ABCD,
∴DE⊥AC,
∵BD 、DE在平面BDE内,且相交于D,
∴AC⊥平面BDE,
∴BE⊥AC.
法二:∵AF⊥平面ABCD,DE∥AF,∴DE⊥平面ABCD,又∵ABCD是正方形,∴DA、DE、DC两两互相垂直,可建立如图的空间直角坐标系,
∴A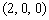 ,C
,C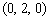 ,B
,B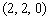 ,E
,E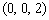 ,
,
∴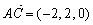 ,
,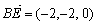 ,
,
∵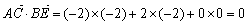 ,∴
,∴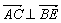 ,即BE⊥AC.
,即BE⊥AC.
(Ⅱ)∵AF⊥平面ABCD,DE∥AF,∴DE⊥平面ABCD,又∵ABCD是正方形,
∴DA、DE、DC两两互相垂直,可建立如图的空间直角坐标系,
∴B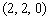 ,C
,C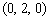 , E
, E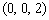 ,D
,D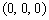 ,
,
∴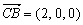 ,
,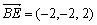 ,
,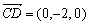 ,
,
∵点N在棱BE上,∴可设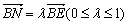 ,
,
∴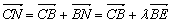 =
=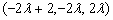 ,
,
由于CD⊥平面ADE,∴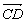 为平面ADE的法向量.
为平面ADE的法向量.
当直线CN与平面ADE成30°角时, 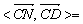 60°,
60°,
∴ 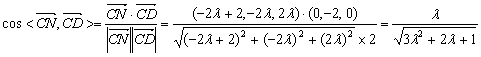 ,
,
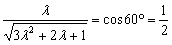 ,解得
,解得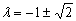 ,∵
,∵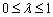 ,∴
,∴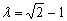 ,---12分
,---12分
∴BN=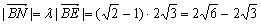 . 4
. 4

练习册系列答案
相关题目
 平面
平面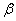 ,那么平面
,那么平面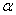 内一定存在直线平行于平面
内一定存在直线平行于平面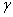 ,平面
,平面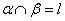 ,那么
,那么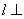 平面
平面 的定义域为 .
的定义域为 .  C.
C.  D.
D. 


 ,
, ,
, ,则 ( ).
,则 ( ). B.
B. C.
C.  D.
D. 
 的定义域为
的定义域为 ,对于任意实数
,对于任意实数 都有
都有 且
且 ,当
,当 时,
时, .若在区间
.若在区间 内,
内, 有且只有4个零点,则实数
有且只有4个零点,则实数 的取值范围是( ).
的取值范围是( ). B.
B. C.
C.  D.
D. 
 的前n项和为Sn,若S3=2,S6=18,则
的前n项和为Sn,若S3=2,S6=18,则 等于( )
等于( ) B. 5 C.
B. 5 C.  31 D.33
31 D.33 ;②
;②
 ;④
;④ ;⑤
;⑤ .
.