题目内容
若关于x的方程2cos2(π+x)-sinx+a=0有实根,求实数a的取值范围.
思路解析:本题是将方程问题与三角函数问题综合设置的一道计算问题,要求解本题,我们必须搞清楚方程的根的关系以及三角函数的范围,在求解过程中还要注意适当变形.
解:原方程变形为2cos2x-sinx+a=0,
即2-2sin2x-sinx+a=0.
∴a=2sin2x+sinx-2=2(sinx+![]() )2-
)2-![]() .
.
∵-1≤sinx≤1,
∴当sinx=-![]() 时,amin=-
时,amin=-![]() ;
;
当sinx=1时,amax=1.
∴a的取值范围是[-![]() ,1].
,1].

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 =(1,1),
=(1,1), =(1,0),<
=(1,0),< ,
, >=
>= 且
且 =-1;若△ABC的内角A,B,C依次成等差数列,且A≤B≤C;
=-1;若△ABC的内角A,B,C依次成等差数列,且A≤B≤C; )=
)= 在[0,B]上有相异实根,求实数m的取值范围;
在[0,B]上有相异实根,求实数m的取值范围; ),试求|
),试求|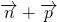 |的取值范围.
|的取值范围.