Question

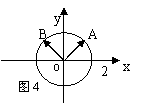
（本小题满分13分）如图，在平面直角坐标系中，A、B为圆x²+y²=4上的点，∠Aox=，∠BoA=β，、β∈(0,π)

(1)若A、B两点分别在第一象限，第二象限，且其纵坐标分别为，求sinβ的值。

（2）若A（－1，）,求函数＝sin(x+)-sinx+1

的单调增区间。

Answer 1

解：（1）依题意得sin ==,cos=

sin(+β)=,cos(+β)=-……………………………………（4分）

∴sinβ=sin[(+β)- ]=…………………（6分）

（2）且∈（0，π）∴ =…………………（8分）

∴＝sin(x+)-sinx+1=-sinx+cosx-sinx=-sinx+cosx+1

=-sin(x-)+1 ………………………………………………（11分）

由2kπ+得2 kπ,k∈Z

∴的单调增区间为[]，k∈Z……………（13分）