题目内容
以下5个命题:
①对实数p和向量 与
与 ,恒有
,恒有 ;
;
②对实数p、q和向量 ,恒有
,恒有 ;
;
③若 ,则
,则 ;
;
④若 ,则p=q;
,则p=q;
⑤对任意的向量 ,恒有
,恒有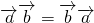 .
.
写出所有真命题的序号________.
①②⑤
分析:根据数乘向量的性质可得①②是真命题,根据向量数量积的定义,可得⑤是真命题.通过举出反例,可以说明③④不一定正确,是假命题.
解答:根据数乘向量的性质,可得
 对任意实数p和向量
对任意实数p和向量 与
与 均成立,故①正确;
均成立,故①正确;
 对任意实数p、q和向量
对任意实数p、q和向量 均成立,故②正确;
均成立,故②正确;
对于③,当实数p为零时,由 ,不能得出
,不能得出 ,故③错;
,故③错;
对于④,当 =
= 时,由
时,由 不能得出p=q,故④错;
不能得出p=q,故④错;
对于⑤,根据向量数量积的定义,可得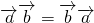 =
= •
• cosθ(θ是它们的夹角),故⑤正确
cosθ(θ是它们的夹角),故⑤正确
故答案为:①②⑤
点评:本题以命题真假的判断为载体,着重考查了向量数量积的定义和数乘向量的定义与性质等知识,属于基础题.
分析:根据数乘向量的性质可得①②是真命题,根据向量数量积的定义,可得⑤是真命题.通过举出反例,可以说明③④不一定正确,是假命题.
解答:根据数乘向量的性质,可得
 对任意实数p和向量
对任意实数p和向量 与
与 均成立,故①正确;
均成立,故①正确; 对任意实数p、q和向量
对任意实数p、q和向量 均成立,故②正确;
均成立,故②正确;对于③,当实数p为零时,由
 ,不能得出
,不能得出 ,故③错;
,故③错;对于④,当
 =
= 时,由
时,由 不能得出p=q,故④错;
不能得出p=q,故④错;对于⑤,根据向量数量积的定义,可得
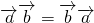 =
= •
• cosθ(θ是它们的夹角),故⑤正确
cosθ(θ是它们的夹角),故⑤正确故答案为:①②⑤
点评:本题以命题真假的判断为载体,着重考查了向量数量积的定义和数乘向量的定义与性质等知识,属于基础题.

练习册系列答案
相关题目