题目内容
已知函数(Ⅰ)求a,c的值;
(Ⅱ)求函数f(x)的单调区间.
解:(Ⅰ)因为函数g(x)=f(x)-2为奇函数,
所以,对任意的x∈R,g(-x)=-g(x),即f(-x)- 2=-f(x)+2.
又f(x)=x3+ax2+3bx+c,
所以-x3+ax2-3bx+c-2=-x3-ax2-3bx-c+2.
所以![]()
解得a=0,c=2.
(Ⅱ)由(Ⅰ)得f(x)=x3+3bx+2.
所以f′(x)=3x2+3b(b≠0).
当b<0时,由f′(x)=0得x=±![]()
x变化时,f′(x)的变化情况如下表:
x | (-∞,- | - | (- |
| ( |
f′(x) | + | 0 | - | 0 | + |
所以,当b<0时,函数f (x)在(-∞,-![]() )上单调递增,在(-
)上单调递增,在(-![]() ,
,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
当b>0时,f′(x)>0.所以函数f (x)在(-∞,+∞)上单调递增.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
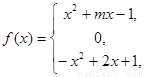
 是奇函数.
是奇函数.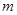 的值;
的值; 在区间
在区间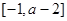 上单调递增,求实数
上单调递增,求实数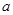 的取值范围;
的取值范围;
 是奇函数.
是奇函数.