题目内容
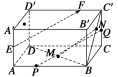
【题目】已知ABCD—A′B′C′D′是平行六面体．
(1)化简
；
(2)设M是底面ABCD的中心，N是侧面BC C′ B′对角线B C′上的
分点，设
，试求α，β，γ的值．
【答案】（1）答案见解析；（2）
.
【解析】
(1)方法一 取AA′的中点为E，取F为D′C′的一个三等分点(D′F＝
D′C′)，由空间向量的运算法则可得
.
方法二 取AB的三等分点P使得
，取CC′的中点Q，由空间向量的运算法则可得 
.
(2)连结BD，则M为BD的中点，由空间向量的结论可得
，则.
(1)方法一 取AA′的中点为E，则
＝
.
又
＝
，
＝
，取F为D′C′的一个三等分点(D′F＝
D′C′)，
则
＝.
∴＋＋＝＋＋＝
.
方法二 取AB的三等分点P使得
＝，
取CC′的中点Q，则＋＋
＝
＋＋＝
＋＋
＝＋＋＝
.
(2)连结BD，则M为BD的中点，
＝
＋
＝
＋
＝ (
＋)＋ (＋)
＝ (－
＋)＋ (＋)＝＋
＋.
∴α＝，β＝，γ＝.
练习册系列答案
相关题目
【题目】探究函数
，x∈(0，+∞)取最小值时x的值，列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题:
(1)函数(x>0)在区间(0，2)上递减；函数
在区间________上递增.当x=_________时，
_______.
(2)证明:函数(x>0)在区间(O，2)上递减.
