题目内容
已知f(x)=x2,g(x)=|x﹣1|,令f1(x)=g(f(x)),fn+1(x)=g(fn(x)),则方程f2015(x)=1解的个数为( )
A. 2014 B. 2015 C. 2016 D. 2017
D
【解析】: 解:∵f(x)=x2,g(x)=|x﹣1|,
∴n=0时:f1(x)=g(x2)=|x2﹣1|,
令|x2﹣1|=1,方程f1(x)有2=0+2个解,
n=1时:f2(x)=g(|x2﹣1|)=||x2﹣1|﹣1|,
令||x2﹣1|﹣1|=1,方程f2(x)有4=2+2个解,
n=2时:f3(x)=|||x2﹣1|﹣1|﹣1|,
令|||x2﹣1|﹣1|﹣1|=1,方程f3(x)有5=3+2个解,
n=3时:f4(x)=||||x2﹣1|﹣1|﹣1|﹣1|,
令||||x2﹣1|﹣1|﹣1|﹣1|=1,方程f4(x)有6=4+2个解,
…,
n=2014时:f2015(x)有2017=2015+2个解,
故选:D.

练习册系列答案
相关题目
通过随机询问110名大学生是否爱好某项运动,得到如下的列联表
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
由上表算得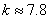 ,因此得到的正确结论是
,因此得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”
 的展开式的各项系数和为729,则
的展开式的各项系数和为729,则 的值为( )
的值为( ) 的虚部是 ( )
的虚部是 ( ) C.
C. D.
D.
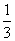 x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0. 的点共有____个.
的点共有____个.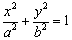
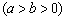 过点
过点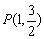 ,其左、右焦点分别为
,其左、右焦点分别为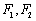 ,离心率
,离心率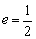 ,
,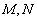 是直线x=4上的两个动点,且
是直线x=4上的两个动点,且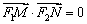 .
.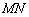 的最小值;
的最小值;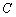 是否过定点?请证明你的结论.
是否过定点?请证明你的结论. 为虚数单位),复数
为虚数单位),复数 的虚部为2,且
的虚部为2,且 是实数,求
是实数,求 中,
中, =2,
=2, ,则
,则 =
=