题目内容
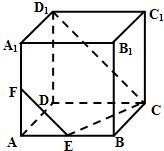
如图所示，在正方体ABCD-A1B1C1D1中E、F分别在A1D、AC上，且A1E=
A1D，AF=
AC，则
- A.EF至多与A1D、AC之一垂直
- B.EF是A1D、AC的公垂线
- C.EF与BD1相交
- D.EF与BD1异面
B
分析：设AC∩BD=O，AD1∩A1D=O1，作EG⊥AD于G，FK⊥AD于K，证明EF⊥AC，EF⊥A1D，即可求得结论．
解答：如图所示
设AC∩BD=O，AD1∩A1D=O1，作EG⊥AD于G，FK⊥AD于K，由平几知识，GF∥DO，DO⊥AC，∴GF⊥AC，
∵EG⊥面ABCD，∴由三垂线逆定理EF⊥AC．
同理EF⊥A1D，
∴EF是A1D、AC公垂线
故选B．
点评：本题考查线面垂直，考查线线位置关系，属于基础题．
分析：设AC∩BD=O，AD1∩A1D=O1，作EG⊥AD于G，FK⊥AD于K，证明EF⊥AC，EF⊥A1D，即可求得结论．
解答：如图所示
设AC∩BD=O，AD1∩A1D=O1，作EG⊥AD于G，FK⊥AD于K，由平几知识，GF∥DO，DO⊥AC，∴GF⊥AC，
∵EG⊥面ABCD，∴由三垂线逆定理EF⊥AC．
同理EF⊥A1D，
∴EF是A1D、AC公垂线
故选B．
点评：本题考查线面垂直，考查线线位置关系，属于基础题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）