题目内容
11.已知函数$f(x)=x+\frac{a}{x}$,且f(1)=2.(1)判断f(x)在[1,+∞)的单调性,并证明你的结论;
(2)求函数在$[{\frac{1}{2},2}]$上最大值和最小值.
分析 (1)由f(1)=2,可得a=1,$f(x)=x+\frac{1}{x}$,f(x)在[1,+∞)上为增函数,运用单调性的定义证明,注意作差、变形和定符号、下结论几个步骤;
(2)可得f(x)在(0,1)递减,求得最小值,比较端点处的函数值,可得最大值.
解答 解:(1)∵由f(1)=2,得a=1,
∴$f(x)=x+\frac{1}{x}$,f(x)在[1,+∞)上为增函数,
下用单调性的定义证明:设1≤x1<x2,
由$f({x_1})-f({x_2})={x_1}+\frac{1}{x_1}-{x_2}-\frac{1}{x_2}$=${x_1}-{x_2}+\frac{{{x_2}-{x_1}}}{{{x_1}{x_2}}}$=$({x_1}-{x_2})\frac{{{x_1}{x_2}-1}}{{{x_1}{x_2}}}$,
∵1≤x1<x2,∴x1-x2<0,x1x2>0,x1x2-1>0,
∴(x1-x2)•$\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}}$<0,即f(x1)-f(x2)<0,得f(x1)<f(x2),
∴f(x)在[1,+∞)上为增函数.
(2)同(1)可证,当0<x1<x2≤1时,
有(x1-x2)•$\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}}$<0,得f(x1)>f(x2),
∴f(x)在(0,1]上为减函数,
∴f(x)在$[{\frac{1}{2},2}]$上有$f{(x)_{max}}=f({\frac{1}{2}})=f(2)=\frac{5}{2}$,
f(x)min=f(1)=2.
点评 本题考查函数的单调性的判断和证明,以及运用:求最值,考查定义法的运用,考查运算能力,属于被揭穿他.

 阅读快车系列答案
阅读快车系列答案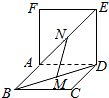 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -24 | B. | 24 | C. | ±24 | D. | -12 |
| A. | f(x)=sinx | B. | f(x)=sin2x | C. | f(x)=cosx | D. | f(x)=cos2x |
 已知四棱锥P-ABCD中,AD=2BC,且AD∥BC,点M,N分别是PB,PD中点,平面MNC交PA于Q.
已知四棱锥P-ABCD中,AD=2BC,且AD∥BC,点M,N分别是PB,PD中点,平面MNC交PA于Q. 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$. 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.