题目内容
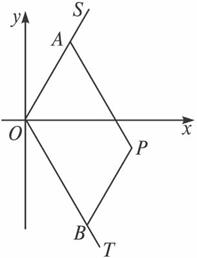
 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等,设OAn=an,若a1=1,a2=2,则数列{an}的通项公式是 .
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等,设OAn=an,若a1=1,a2=2,则数列{an}的通项公式是 .
【答案】分析:设 ,利用已知可得A1B1是三角形OA2B2的中位线,得到
,利用已知可得A1B1是三角形OA2B2的中位线,得到 =
= =
= ,梯形A1B1B2A2的面积=3S.由已知可得梯形AnBnBn+1An+1的面积=3S.利用相似三角形的性质面积的比等于相似比的平方可得:
,梯形A1B1B2A2的面积=3S.由已知可得梯形AnBnBn+1An+1的面积=3S.利用相似三角形的性质面积的比等于相似比的平方可得: ,
, ,
, ,…,已知
,…,已知 ,
, ,可得
,可得 ,….因此数列{
,….因此数列{ }是一个首项为1,公差为3等差数列,即可得到an.
}是一个首项为1,公差为3等差数列,即可得到an.
解答:解:设 ,∵OA1=a1=1,OA2=a2=2,A1B1∥A2B2,
,∵OA1=a1=1,OA2=a2=2,A1B1∥A2B2,
∴A1B1是三角形OA2B2的中位线,∴ =
= =
= ,∴梯形A1B1B2A2的面积=3S.
,∴梯形A1B1B2A2的面积=3S.
故梯形AnBnBn+1An+1的面积=3S.
∵所有AnBn相互平行,∴所有△OAnBn(n∈N*)都相似,∴ ,
, ,
, ,…,
,…,
∵ ,∴
,∴ ,
, ,….
,….
∴数列{ }是一个等差数列,其公差d=3,故
}是一个等差数列,其公差d=3,故 =1+(n-1)×3=3n-2.
=1+(n-1)×3=3n-2.
∴ .
.
因此数列{an}的通项公式是 .
.
故答案为 .
.
点评:本题综合考查了三角形的中位线定理、相似三角形的性质、等差数列的通项公式等基础知识和基本技能,考查了推理能力和计算能力.
 ,利用已知可得A1B1是三角形OA2B2的中位线,得到
,利用已知可得A1B1是三角形OA2B2的中位线,得到 =
= =
= ,梯形A1B1B2A2的面积=3S.由已知可得梯形AnBnBn+1An+1的面积=3S.利用相似三角形的性质面积的比等于相似比的平方可得:
,梯形A1B1B2A2的面积=3S.由已知可得梯形AnBnBn+1An+1的面积=3S.利用相似三角形的性质面积的比等于相似比的平方可得: ,
, ,
, ,…,已知
,…,已知 ,
, ,可得
,可得 ,….因此数列{
,….因此数列{ }是一个首项为1,公差为3等差数列,即可得到an.
}是一个首项为1,公差为3等差数列,即可得到an.解答:解:设
 ,∵OA1=a1=1,OA2=a2=2,A1B1∥A2B2,
,∵OA1=a1=1,OA2=a2=2,A1B1∥A2B2,∴A1B1是三角形OA2B2的中位线,∴
 =
= =
= ,∴梯形A1B1B2A2的面积=3S.
,∴梯形A1B1B2A2的面积=3S.故梯形AnBnBn+1An+1的面积=3S.
∵所有AnBn相互平行,∴所有△OAnBn(n∈N*)都相似,∴
 ,
, ,
, ,…,
,…,∵
 ,∴
,∴ ,
, ,….
,….∴数列{
 }是一个等差数列,其公差d=3,故
}是一个等差数列,其公差d=3,故 =1+(n-1)×3=3n-2.
=1+(n-1)×3=3n-2.∴
 .
.因此数列{an}的通项公式是
 .
.故答案为
 .
.点评:本题综合考查了三角形的中位线定理、相似三角形的性质、等差数列的通项公式等基础知识和基本技能,考查了推理能力和计算能力.

练习册系列答案
相关题目
 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC, (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,