题目内容
已知函数f(x)在定义域(0,+∞)上单调递增,且满足f(xy)=f(x)+f(y).(1)证明:f(
| x | y |
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
分析:(1)结合抽象表达式用
代替x,y不变,即可转化即可获得问题f(
)=f(x)-f(y)的解答;
(2)首先利用数值的搭配计算f(9)=2,进而对不等式进行转化,然后结合函数y=f(x)是定义在(0,+∞)上的单调性,结合变形后的抽象函数即可获得变量a的要求,进而问题即可获得解答.
| x |
| y |
| x |
| y |
(2)首先利用数值的搭配计算f(9)=2,进而对不等式进行转化,然后结合函数y=f(x)是定义在(0,+∞)上的单调性,结合变形后的抽象函数即可获得变量a的要求,进而问题即可获得解答.
解答:解:(1)∵对一切x,y>0满足f(x)+f(y)=f(x•y),
∴f(
)+f(y)=f(
×y)=f(x)
因此,满足 f(
)=f(x)-f(y),
(2)∵f(3)=1,∴2=f(3)+f(3)=f(9);
∵f(x)是定义在(0,+∞)上的增函数,
∴f(a)>f(a-1)+2,?
?
?1<a<
,
故a的取值范围(1,
)
∴f(
| x |
| y |
| x |
| y |
因此,满足 f(
| x |
| y |
(2)∵f(3)=1,∴2=f(3)+f(3)=f(9);
∵f(x)是定义在(0,+∞)上的增函数,
∴f(a)>f(a-1)+2,?
|
|
?1<a<
| 9 |
| 8 |
故a的取值范围(1,
| 9 |
| 8 |
点评:本题考查的是抽象函数及其应用的综合类问题.在解答的过程当中充分体现了定义域优先的原则、特值的思想、转化的思想以及计算和解不等式组的能力.值得同学们体会和反思.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
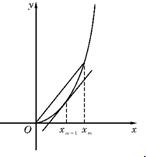 已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.