题目内容
(Ⅰ)已知k∈N,n∈N*,且 k≤n,求证: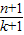
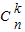 =
=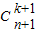 ;
;(Ⅱ) 若(n+1)
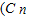
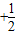
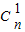
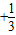
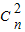
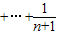
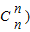 =31,试求n的值,并求(1+x)2n的展开式中系数最大的项.
=31,试求n的值,并求(1+x)2n的展开式中系数最大的项.
【答案】分析:(Ⅰ)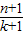
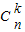 =
=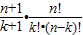 ,由此能够证明
,由此能够证明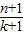
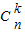 =
=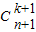 .
.
(Ⅱ)由(n+1)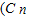
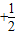
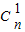
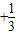
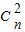
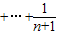
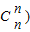 =31,能够推导出2n+1-1=31,解得n=4.故(1+x)2n=(1+x)8展开式中系数最大的项是第5项,由此能求出(1+x)2n的展开式中系数最大的项.
=31,能够推导出2n+1-1=31,解得n=4.故(1+x)2n=(1+x)8展开式中系数最大的项是第5项,由此能求出(1+x)2n的展开式中系数最大的项.
解答:(Ⅰ)证明: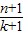
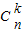 =
=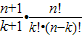
=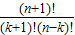 =
=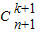 ,
,
∴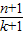
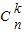 =
=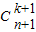 .
.
(Ⅱ)解:∵(n+1)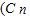
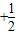
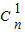
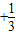
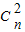
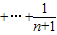
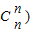 =31,
=31,
∴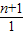
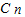 +
+ +
+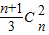 +…+
+…+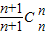
= +…+
+…+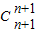
=2n+1-1,
∴2n+1-1=31,
∴2n+1=32,解得n=4.
∴(1+x)2n=(1+x)8展开式中系数最大的项是第5项,
则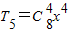 =70x4,
=70x4,
∴(1+x)2n的展开式中系数最大的项为70x4.
点评:本题考查组合数的证明,考查展开式中系数最大的项的求法.解题时要认真审题,仔细解答,注意组合数公式的灵活运用.
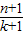
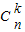 =
=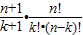 ,由此能够证明
,由此能够证明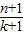
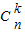 =
=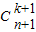 .
.(Ⅱ)由(n+1)
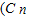
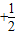
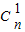
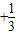
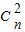
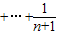
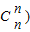 =31,能够推导出2n+1-1=31,解得n=4.故(1+x)2n=(1+x)8展开式中系数最大的项是第5项,由此能求出(1+x)2n的展开式中系数最大的项.
=31,能够推导出2n+1-1=31,解得n=4.故(1+x)2n=(1+x)8展开式中系数最大的项是第5项,由此能求出(1+x)2n的展开式中系数最大的项.解答:(Ⅰ)证明:
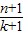
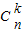 =
=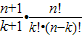
=
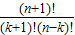 =
=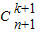 ,
,∴
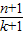
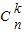 =
=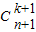 .
.(Ⅱ)解:∵(n+1)
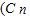
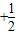
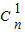
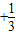
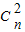
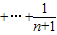
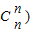 =31,
=31,∴
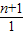
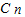 +
+ +
+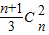 +…+
+…+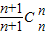
=
 +…+
+…+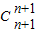
=2n+1-1,
∴2n+1-1=31,
∴2n+1=32,解得n=4.
∴(1+x)2n=(1+x)8展开式中系数最大的项是第5项,
则
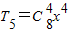 =70x4,
=70x4,∴(1+x)2n的展开式中系数最大的项为70x4.
点评:本题考查组合数的证明,考查展开式中系数最大的项的求法.解题时要认真审题,仔细解答,注意组合数公式的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
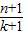
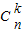 =
=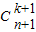 ;
;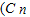
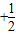
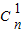
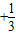
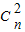
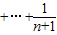
 =31,试求n的值,并求(1+x)2n的展开式中系数最大的项.
=31,试求n的值,并求(1+x)2n的展开式中系数最大的项.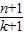
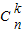 =
=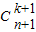 ;
;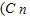
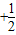
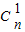
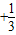
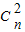
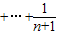
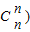 =31,试求n的值,并求(1+x)2n的展开式中系数最大的项.
=31,试求n的值,并求(1+x)2n的展开式中系数最大的项.