题目内容
对于函数f(x)=(2x﹣x2)ex
(1)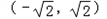 是f(x)的单调递减区间;
是f(x)的单调递减区间;
(2)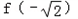 是f(x)的极小值,
是f(x)的极小值,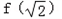 是f(x)的极大值;
是f(x)的极大值;
(3)f(x)有最大值,没有最小值;
(4)f(x)没有最大值,也没有最小值.
其中判断正确的是( ).
(1)
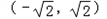 是f(x)的单调递减区间;
是f(x)的单调递减区间;(2)
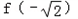 是f(x)的极小值,
是f(x)的极小值,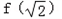 是f(x)的极大值;
是f(x)的极大值;(3)f(x)有最大值,没有最小值;
(4)f(x)没有最大值,也没有最小值.
其中判断正确的是( ).
(2)(3)

练习册系列答案
相关题目