题目内容
写出求m=60和n=33的最大公约数的算法和程序框图.
答案:略
解析:
解析:
|
【解法一】算法: S1 :以n除m,得余数r=27;S2 :判断r是否为零,若r=0,则n为解.若 r≠0,则重复S3操作(r=27);S3 :以n作为新的m(33),以r作为新的n(27),求新的m/n的余数r=6;S4 :判断r是否为零,若r=0,则前一个n即为解.否则要继续 S5的操作;S5 :以n作为新的m(即m=27),以r作为新的n(即n=6).求新的余数 r=3;S6 :判断上一个r是否为零,若r=0,则前一个n即为解,否则要执行S7操作;S7 :以n作为新的m(m=6),r 作为新的n(n=3),求新的r=0;S8 :判断r是否为零,这里r=0,算法结束得n=3是60与33的最大公约数.程序框图略 【解法二】算法: S1 :输入60,33,将m=60,n=33;S2 :求m/n余数r;S3 :若r=0,则n就是所求最大公约,输出n.若r≠0,执行下一步;S4 :使n作为新的m,使r作为新的n,执行S2.程序框图 (当型):
【解法三】算法: S1 :令m=60,n=33;S2 :重复执行下面序列,直到求得r=0为止;S3 :求m/n的余数r;S4 :令m=n,n=r;S5 :输出m.程序框图 (直到型):
|

练习册系列答案
相关题目


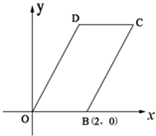 如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.
如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.