题目内容
四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形且∠ADC=60°.
(1)求证:PA⊥CD;
(2)求二面角P-AB-D的大小.
(1)求证:PA⊥CD;
(2)求二面角P-AB-D的大小.
(1)作PO⊥CD于O,连接OA
由侧面PDC与底面ABCD垂直,则PO⊥面ABCD
所以PO⊥OA且PO⊥OC,又由∠ADC=60°,DO=1,AD=2,
则∠DOA=90°,即OA⊥CD
分别以OA,OC,OP所在直线为x轴,y轴,z轴建立空间直角坐标系,
由已知P(0,0,
),A(
,0,0),D(0,-1,0),C(0,1,0),
∴
=(
,0,-
),
=(0,-2,0),
∴
•
=0,∴
⊥
,
∴PA⊥CD.
(2)∵P(0,0,
),A(
,0,0),B(
,2,0),D(0,-1,0),
∴
=(
,0,-
),
=(
,2,-
),
=(
,1,0),
=(
,3,0)
设平面ABP的法向量为
=(x1,y1,z1),则
•
=0,
•
=0,
∴
,解得
=(1,0,1).
设平面ABD的法向量为
=(x2,y2,z2),则
•
=0,
•
=0,
∴
,解得
=(0,0,1),
设二面角P-AB-D的平面角为θ,
则cosθ=|cos<
,
>|=|
|=
,
∴θ=45°,
故二面角P-AB-D的大小为45°.
由侧面PDC与底面ABCD垂直,则PO⊥面ABCD
所以PO⊥OA且PO⊥OC,又由∠ADC=60°,DO=1,AD=2,
则∠DOA=90°,即OA⊥CD
分别以OA,OC,OP所在直线为x轴,y轴,z轴建立空间直角坐标系,
由已知P(0,0,
| 3 |
| 3 |
∴
| PA |
| 3 |
| 3 |
| CD |
∴
| PA |
| CD |
| PA |
| CD |
∴PA⊥CD.
(2)∵P(0,0,
| 3 |
| 3 |
| 3 |
∴
| PA |
| 3 |
| 3 |
| PB |
| 3 |
| 3 |
| DA |
| 3 |
| DB |
| 3 |
设平面ABP的法向量为
| m |
| m |
| PA |
| m |
| PB |
∴
|
| m |
设平面ABD的法向量为
| n |
| n |
| DA |
| n |
| DB |
∴
|
| n |
设二面角P-AB-D的平面角为θ,
则cosθ=|cos<
| m |
| n |
| 1 | ||
|
| ||
| 2 |
∴θ=45°,
故二面角P-AB-D的大小为45°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
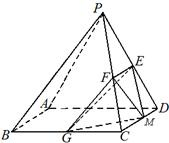 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.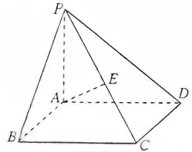 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2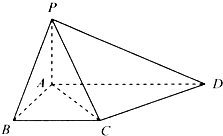 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.