题目内容
设 ,
, ,
, ,且
,且 ,则
,则 的最小值为 .
的最小值为 .
【答案】分析: ,
, ,且
,且 ,则两向量垂直,则当
,则两向量垂直,则当 与
与 反向时,
反向时, 有最小值.
有最小值.
解答:解:∵ ,
, ,且
,且 ,
,
∴
∴
则当 与
与 反向时
反向时
 =-
=-
故答案为:
点评:本题考查的是两个向量数量积的最值问题: =
= cosθ
cosθ
当θ=0,即两向量同向时,cosθ=1时, =
= 有最大值;
有最大值;
当θ=π,即两向量反向时,cosθ=-1时, =-
=- 有最小值
有最小值
 ,
, ,且
,且 ,则两向量垂直,则当
,则两向量垂直,则当 与
与 反向时,
反向时, 有最小值.
有最小值.解答:解:∵
 ,
, ,且
,且 ,
,∴

∴

则当
 与
与 反向时
反向时 =-
=-
故答案为:

点评:本题考查的是两个向量数量积的最值问题:
 =
= cosθ
cosθ当θ=0,即两向量同向时,cosθ=1时,
 =
= 有最大值;
有最大值;当θ=π,即两向量反向时,cosθ=-1时,
 =-
=- 有最小值
有最小值 
练习册系列答案
相关题目
 ,
, 且
且 ,则
,则 的最小值是
.
的最小值是
. 均不小于1,且
均不小于1,且 ,则
,则 的最小值是 .(
的最小值是 .( 是指
是指 四个数中最大的一个)
四个数中最大的一个) 均为正实数,且
均为正实数,且 ,则
,则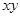 的最小值为____________.
的最小值为____________.