题目内容
已知函数f(x)=ln(1+x2)+ax.(a≤0).
(Ⅰ)若f(x)在x=0处取得极值,求a的值;
(Ⅱ)讨论f(x)的单调性;
(Ⅲ)证明: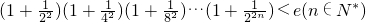 .
.
解:(Ⅰ) ,因为x=0是f(x)的一个极值点,∴f'(0)=0,∴a=0验证知a=0符合条件.------------2分
,因为x=0是f(x)的一个极值点,∴f'(0)=0,∴a=0验证知a=0符合条件.------------2分
(Ⅱ)因为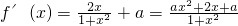
1)若a=0时,∴f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;
2)若 ,∴f(x)在R上单调递减;
,∴f(x)在R上单调递减;
3)若-1<a<0时,由f'(x)>0得ax2+2x+a>0∴ ∴
∴ ,
,
在 ;
;
综上所述,若a≤-1时,f(x)在(-∞,+∞)上单调递减,
若-1<a<0时, ,
,
若a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减.---------8分
(Ⅲ)由(Ⅱ)知,当a=-1时,f(x)在(-∞,+∞)单调递减
当x∈(0,+∞)时,由f(x)<f(0)=0∴ln(1+x2)<x
∴

∴ ---------------------13分
---------------------13分
分析:(Ⅰ)求出f′(x),因为f(x)在x=0时取得极值,所以f'(0)=0,代入求出a即可;
(Ⅱ)分三种情况:a=0;a≤-1;-1<a<0,令f′(x)>0得到函数的递增区间;令f′(x)<0得到函数的递减区间即可;(Ⅲ)由(2)知当a=-1时函数为减函数,所以得到ln(1+x2)<x,利用这个结论根据对数的运算法则化简不等式的左边得证即可.
点评:考查学生利用导数研究函数单调性的能力,以及会用待定系数法求函数解析式,会利用单调性及对数函数运算证明不等式.会求等比数列的前n项的和.以及利用导数研究函数极值的能力.
 ,因为x=0是f(x)的一个极值点,∴f'(0)=0,∴a=0验证知a=0符合条件.------------2分
,因为x=0是f(x)的一个极值点,∴f'(0)=0,∴a=0验证知a=0符合条件.------------2分(Ⅱ)因为
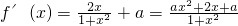
1)若a=0时,∴f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;
2)若
 ,∴f(x)在R上单调递减;
,∴f(x)在R上单调递减;3)若-1<a<0时,由f'(x)>0得ax2+2x+a>0∴
 ∴
∴ ,
,在
 ;
;综上所述,若a≤-1时,f(x)在(-∞,+∞)上单调递减,
若-1<a<0时,
 ,
,
若a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减.---------8分
(Ⅲ)由(Ⅱ)知,当a=-1时,f(x)在(-∞,+∞)单调递减
当x∈(0,+∞)时,由f(x)<f(0)=0∴ln(1+x2)<x
∴


∴
 ---------------------13分
---------------------13分分析:(Ⅰ)求出f′(x),因为f(x)在x=0时取得极值,所以f'(0)=0,代入求出a即可;
(Ⅱ)分三种情况:a=0;a≤-1;-1<a<0,令f′(x)>0得到函数的递增区间;令f′(x)<0得到函数的递减区间即可;(Ⅲ)由(2)知当a=-1时函数为减函数,所以得到ln(1+x2)<x,利用这个结论根据对数的运算法则化简不等式的左边得证即可.
点评:考查学生利用导数研究函数单调性的能力,以及会用待定系数法求函数解析式,会利用单调性及对数函数运算证明不等式.会求等比数列的前n项的和.以及利用导数研究函数极值的能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目