Question

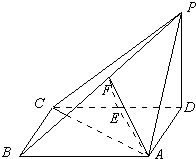如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．
（1）求证：EF⊥面PAB；
（2）若AB=

2

BC，求AC与面AEF所成的角．

Answer 1

分析：方法一：（1）取PA中点G，连接FG，DG，证明DG⊥平面PABDE，根据FE∥DG，得出EF⊥面PAB；
（2）由图形知线面角不易做出，但斜线AC的长度易求出，且可用等体积法算出C到而AEF的距离，如此则可以算出线面角的正弦值．此法省却了作图的麻烦．
方法二：由题设建立空间坐标系比较方便，故可用空间向量法解决，（1）求出直线的方向向量与面的法向量，证明其内积为0即可．（2）求出面的法向量与线的方向向量，按规则求出线面角即可．

解答：解：方法一：
（1）取PA中点G，连接FG，DG

BF=FP?FG ∥ . 1 2 AB CE=ED?DE ∥ . 1 2 AB

?FG

∥

.

DE
?四边形DEFG为平行四边形?EF

∥ .

.

DG
?平面PAB⊥平面PAD
又PD=AD，PG=GA?DG⊥PA
?DG⊥平面PABDE，又FE∥DG
?EF⊥平面PAB．（6分）
（2）设AC，BD交于O，连接FO．
由PF=BF，BO=OD得FO

∥ .

.

1

2

PD，又PD⊥平面ABCD
∴FO⊥平面ABCD
设BC=a，则AB=

2

a，∴PA=

2

a，
DG=

2

2

a=EF，∴PB=2a，AF=a．
设C到平面AEF的距离为h．
∵V_C-AEF=V_F-ACE，∴

1

3

×

1

2

EF•AF•h=

1

3

×

1

2

CE•AD•FO
即

2

2

a•a•h=

2

2

a•a•

a

2

∴h=

a

2

∴AC与平面AEF所成角的正弦值为

h

AC

=

a/2

3 a

=

3

6

．
即AC与平面AEF所成角为arcsin

3

6

（12分）
方法二：以D为坐标原点，DA的长为单位，建立如图所示的直角坐标系，
（1）证明：
设E（a，0，0），其中a＞0，则C(2a，0，0)，A(0，1，0)，B(2a，1，0)，P(0，0，1)，F(a，

1

2

，

1

2

)，

EF

=(0，

1

2

，

1

2

)，

PB

=(2a，1，-1)，

AB

=(2a，0，0)，

EF

•

PB

=0，∴EF⊥PB，

AB

•

EF

=0，∴AB⊥EF
又PB?平面PAB，AB?平面PAB，PB∩AB=B，∴EF⊥?平面PAB（6分）
（2）解：由AB=

2

BC，得a=

2

2

，
可得

AC

=(

2

，-1，0)，

PB

=(

2

，1，-1)
cos?

AC

，

PB

＞=

AC • PB

| AC |•| PB |

=

3

6

，
则异面直线AC，PB所成的角为arccos

3

6

，

AF

=(

2

2

，-

1

2

，

1

2

)，∴

AF

•

PB

=0，AF⊥PB，
又PB⊥EF，AF为平面AEF内两条相交直线，
∴PB⊥平面AEF，∴AC与平面AEF所成的角为

π

2

-arccos

3

6

(=arcsin

3

6

)，
即AC与平面AEF所成的角为arcsin

3

6

．（12分）

点评：考查用几何法与向量法证明空间几何体中的线面垂直问题及求线面夹角的问题．