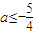题目内容
为使方程cos2x-sinx+a=0在
内有解，则a的取值范围是（ ）A．-1≤a≤1
B．-1＜a≤1
C．-1≤a＜0
D．
【答案】分析：本题宜变为求三角函数的值域的问题，可令a=-cos2x+sinx，求其值域即得参数a取值范围
解答：解：由题意，方程可变为a=-cos2x+sinx
令t=sinx，由0＜x≤
得t=sinx∈（0，1]
即a=t2+t-1，t∈（0，1]
解得a∈（-1，1]
故选B
点评：本题的考点是复合函数的单调性，考查根据复合三角函数的单调性求值域，本题求参数范围的题转化为求函数的值域是解此类题的常用技巧．
解答：解：由题意，方程可变为a=-cos2x+sinx
令t=sinx，由0＜x≤
得t=sinx∈（0，1]即a=t2+t-1，t∈（0，1]
解得a∈（-1，1]
故选B
点评：本题的考点是复合函数的单调性，考查根据复合三角函数的单调性求值域，本题求参数范围的题转化为求函数的值域是解此类题的常用技巧．
练习册系列答案
阅读快车系列答案
相关题目
为使方程cos2x-sinx+a=0在(0，
]内有解，则a的取值范围是（ ）
| π |
| 2 |
| A、-1≤a≤1 | ||
| B、-1＜a≤1 | ||
| C、-1≤a＜0 | ||
D、a≤-
|
内有解，则a的取值范围是（ ）
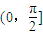内有解，则a的取值范围是（ ）