题目内容
【题目】已知函数![]()
(1)![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)对任意的![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求![]() ,由导数的几何意义可得
,由导数的几何意义可得![]() ,求出
,求出![]() ,求出
,求出![]() ,把点
,把点![]() 代入切线方程,求出图;
代入切线方程,求出图;
(2)对任意的![]() ,
,![]() 恒成立,等价不等式
恒成立,等价不等式![]() 对任意的
对任意的![]() 恒成立. 令
恒成立. 令![]() ,只需
,只需![]() .求
.求![]() ,对
,对![]() 分类讨论,利用
分类讨论,利用![]() 的单调性求解.
的单调性求解.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
由导数的几何意义可得![]() ,即
,即![]() .
.
![]() ,
,
把点![]() 代入切线方程
代入切线方程![]() ,得
,得![]() .
.
![]() .
.
(2)对任意的![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
等价于![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 单调递增,
单调递增,
![]() 恒成立,
恒成立,
故![]() 满足题意.
满足题意.
当![]() 时,令
时,令![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() .
.
令![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 单调递减,
单调递减,![]()
![]() ,与
,与![]() 对任意的
对任意的![]() 恒成立矛盾,
恒成立矛盾,
故![]() 不合题意,舍去.
不合题意,舍去.
综上,![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】在新高考改革中,打破了文理分科的“![]() ”模式,不少省份采用了“
”模式,不少省份采用了“![]() ”,“
”,“![]() ”,“
”,“![]() ”等模式.其中“
”等模式.其中“![]() ”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含男生110人,求n的值及抽取到的女生人数;
(2)在(1)的情况下对抽取到的n名同学“选物理”和“选历史”进行问卷调查,得到下列2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选科目与性别有关?
选物理 | 选历史 | 合计 | |
男生 | 90 | ||
女生 | 30 | ||
合计 |
(3)在(2)的条件下,从抽取的“选历史”的学生中按性别分层抽样再抽取5名,再从这5名学生中抽取2人了解选政治、地理、化学、生物的情况,求2人至少有1名男生的概率.
参考公式: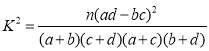 .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |

