题目内容
有下列四个命题:①
 的最小值是
的最小值是 ;
;②已知
 ,则f(4)<f(3);
,则f(4)<f(3);③y=loga(2+ax)(a>0,a≠1)在定义域R上是增函数;
④定义在实数集R上的奇函数f(x)满足f(x+1)=-f(x),则f(2)=0.
其中,真命题的序号是 .(把你认为正确命题的序号都填上)
【答案】分析:遵循正确的给出证明错误的给出一个反例的原则即可作出判断.
解答:解:①令t=sin2x则t∈(0,1]所以 =t+
=t+ 在(0,1]上单调递减故y的最小值是4故①错
在(0,1]上单调递减故y的最小值是4故①错
②由于 =1-
=1- 且4-
且4- >0>3-
>0>3- 则f(4)<f(3)故②对
则f(4)<f(3)故②对
③由于y=loga(2+ax)(a>0,a≠1)可看作由y=logat,t=2+ax复合而成而当a∈(0,1),a∈(1,+∞)y=logat,t=2+ax的单调性相同故根据复合函数单调性的判断法则“同增异减”即可判断出y=loga(2+ax)(a>0,a≠1)在定义域R上是增函数故③对
④根据f(x+1)=-f(x)可得f(2)=-f(1)且f(1)=-f(0)而函数f(x)是定义在实数集R上的奇函数则有f(0)=0所以f(2)=0故④对
故答案为②③④
点评:本题主要考查了命题真假的判断.解题的关键是把握住此类问题的判断准则“正确的给出证明,错误的举出反例”!
解答:解:①令t=sin2x则t∈(0,1]所以
 =t+
=t+ 在(0,1]上单调递减故y的最小值是4故①错
在(0,1]上单调递减故y的最小值是4故①错②由于
 =1-
=1- 且4-
且4- >0>3-
>0>3- 则f(4)<f(3)故②对
则f(4)<f(3)故②对③由于y=loga(2+ax)(a>0,a≠1)可看作由y=logat,t=2+ax复合而成而当a∈(0,1),a∈(1,+∞)y=logat,t=2+ax的单调性相同故根据复合函数单调性的判断法则“同增异减”即可判断出y=loga(2+ax)(a>0,a≠1)在定义域R上是增函数故③对
④根据f(x+1)=-f(x)可得f(2)=-f(1)且f(1)=-f(0)而函数f(x)是定义在实数集R上的奇函数则有f(0)=0所以f(2)=0故④对
故答案为②③④
点评:本题主要考查了命题真假的判断.解题的关键是把握住此类问题的判断准则“正确的给出证明,错误的举出反例”!

练习册系列答案
相关题目
 8、
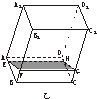
8、 如图甲,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题:
如图甲,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题: