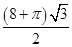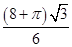题目内容
正方形 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边 、
、 上,且
上,且 ,
, ,将此正
,将此正
方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥 的体积是( )
的体积是( )
A. | B. | C. | D. |
B
解析试题分析:解:因为 所以
所以
又因为 平面
平面 ,
, 平面
平面 ,且
,且 ,所以
,所以 平面
平面
在 中,
中,
所以 ,
,
所以

所以应选B.
考点:1、直线与平面垂直的判定;2、正弦定理与余弦定理;3、棱锥的体积.

练习册系列答案
相关题目
如图,某几何体的正视图是平行四边形,侧视图和俯视图都是矩形,则该几何体的体积为( )
A.6 | B.9 | C.8 | D.12 |
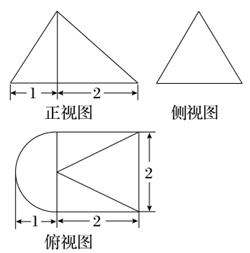
已知空间几何体的三视图如图所示,则该几何体的体积是( )
A. | B. | C.4 | D. |
[2013·江西高考]一几何体的三视图如图所示,则该几何体的体积为( )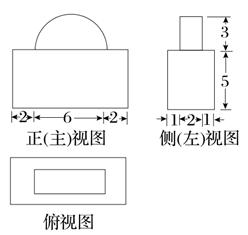
| A.200+9π | B.200+18π | C.140+9π | D.140+18π |
棱长为2的三棱锥的外接球的表面积为( )
| A.6π | B.4π | C.2π | D.π |






 与高
与高 ,计算其体积
,计算其体积 的近似公式
的近似公式 它实际上是将圆锥体积公式中的圆周率
它实际上是将圆锥体积公式中的圆周率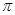 近似取为3.那么近似公式
近似取为3.那么近似公式 相当于将圆锥体积公式中的
相当于将圆锥体积公式中的