题目内容
若正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线y2=2px（p＞0）上，则这个正三角形的面积是（ ）A．
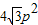
B．
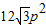
C．48p2
D．36p2
【答案】分析：设另外两个顶点的坐标分别为（ a，
a）、（ a，-
a），代入抛物线方程可得 
=2pa，解得 a=6p，可得正三角形的边长为 
a=4
p，
由此求得这个正三角形的面积．
解答：解：由题意可得，正三角形的另外两个顶点关于x轴对称，设另外两个顶点的坐标分别为（ a，
a）、（ a，-
a），
把顶点（ a，
a） 代入抛物线方程可得 
=2pa，解得a=6p，故正三角形的边长为 
a=4
p，
故这个正三角形的面积是
•4
p•4
p•sin60°=12
p2，
故选B．
点评：本题主要考查抛物线的定义、标准方程，以及简单性质的应用，属于中档题．
a）、（ a，-a），代入抛物线方程可得 =2pa，解得 a=6p，可得正三角形的边长为 a=4p，由此求得这个正三角形的面积．
解答：解：由题意可得，正三角形的另外两个顶点关于x轴对称，设另外两个顶点的坐标分别为（ a，
a）、（ a，-a），把顶点（ a，
a） 代入抛物线方程可得 =2pa，解得a=6p，故正三角形的边长为 a=4p，故这个正三角形的面积是
•4p•4p•sin60°=12p2，故选B．
点评：本题主要考查抛物线的定义、标准方程，以及简单性质的应用，属于中档题．
练习册系列答案
相关题目
p2
p2
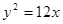上，则这个三角形的面积为 。