题目内容
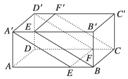
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
(1)求异面直线A1M和C1D1所成的角的正切值;
(2)证明:平面ABM⊥平面A1B1M。
(1)求异面直线A1M和C1D1所成的角的正切值;
(2)证明:平面ABM⊥平面A1B1M。

(1)解:因为C1D1∥B1A1,所以∠MA1B1为异面直线A1M与C1D1所成的角,
因为A1B1⊥平面BCC1B1,所以∠A1B1M=90°,
而A1B1=1,B1M=
故tan∠MA1B1= ,
,
即异面直线A1M和C1D1所成的角的正切值为 。
。
(2)证明:由A1B1⊥平面BCC1B1,BM 平面BCC1B1,得A1B1⊥BM, ①
平面BCC1B1,得A1B1⊥BM, ①
由(1)知,B1M= ,
,
又BM= ,B1B=2,所以
,B1B=2,所以 ,
,
从而BM⊥B1M, ②
又A1B1∩B1M=B1,再由①②得BM⊥平面A1B1M,
而BM 平面ABM,
平面ABM,
因此平面ABM⊥平面A1B1M。
因为A1B1⊥平面BCC1B1,所以∠A1B1M=90°,
而A1B1=1,B1M=

故tan∠MA1B1=
 ,
,即异面直线A1M和C1D1所成的角的正切值为
 。
。(2)证明:由A1B1⊥平面BCC1B1,BM
 平面BCC1B1,得A1B1⊥BM, ①
平面BCC1B1,得A1B1⊥BM, ① 由(1)知,B1M=
 ,
,又BM=
 ,B1B=2,所以
,B1B=2,所以 ,
,从而BM⊥B1M, ②
又A1B1∩B1M=B1,再由①②得BM⊥平面A1B1M,
而BM
 平面ABM,
平面ABM,因此平面ABM⊥平面A1B1M。

练习册系列答案
相关题目
 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.