题目内容
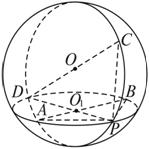
球面上有四个点P，A，B，C，PA，PB，PC两两互相垂直，PA=PB=PC=1，则该球的表面积是（ ）
分析：根据题意，分别以PA、PB、PC为长、宽、高作出正方体，求出该正方体的外接球表面积，即为本题所求表面积
解答：解：∵PA、PB、PC两两互相垂直，且PA=PB=PC=1，
∴分别以PA、PB、PC为长、宽、高，作出正方体
设所得正方体的外接球为球O，则P、A、B、C四点所在的球面就是球O表面
就是正方体的对角线长等于球O的直径，即2R=
=
，得R=
，
∴球的表面积为S=4πR2=4π（
）2=3π，
故答案是3π．
∴分别以PA、PB、PC为长、宽、高，作出正方体
设所得正方体的外接球为球O，则P、A、B、C四点所在的球面就是球O表面
就是正方体的对角线长等于球O的直径，即2R=
| PA2+PB2+PC2 |
| 3 |
| ||
| 2 |
∴球的表面积为S=4πR2=4π（
| ||
| 2 |
故答案是3π．
点评：本题着重考查了球内接多面体和球的表面积公式等知识，根据内接几何体的性质求球的半径是关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
