题目内容
已知函数y=sin6x+cos6x (x∈R),用公式a3+b3=(a+b)(a2-ab+b2)将其化简,并求其周期、最小值和单调递减区间.
【答案】分析:利用公式a3+b3=(a+b)(a2-ab+b2)将函数y=sin6x+cos6x (x∈R),化简为y= +
+ cos4x,从而可求其周期、最小值和单调递减区间.
cos4x,从而可求其周期、最小值和单调递减区间.
解答:解:∵y=sin6x+cos6x=(sin2x+cos2x)(sin4x-sin2xcos2x+cos4x)
=1•(sin2x+cos2x)2-3sin2xcos2x
=1- sin22x
sin22x
= +
+ cos4x…(6分),
cos4x…(6分),
∴周期T=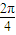 …(7分),
…(7分),
最小值为: -
- =
= …(9分)
…(9分)
由2kπ≤4x≤2kπ+π,(k∈Z)得: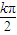 ≤x≤
≤x≤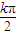 +
+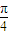 ,(k∈Z)
,(k∈Z)
∴单调递减区间[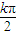 ,
,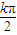 +
+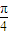 ],(k∈Z)…(12分) 注:丢掉k∈Z扣1分.
],(k∈Z)…(12分) 注:丢掉k∈Z扣1分.
点评:本题考查二倍角的余弦,三角函数的平方关系式及三角函数的周期性及其求法,突出考查余弦函数的单调性,属于中档题.
 +
+ cos4x,从而可求其周期、最小值和单调递减区间.
cos4x,从而可求其周期、最小值和单调递减区间.解答:解:∵y=sin6x+cos6x=(sin2x+cos2x)(sin4x-sin2xcos2x+cos4x)
=1•(sin2x+cos2x)2-3sin2xcos2x
=1-
 sin22x
sin22x=
 +
+ cos4x…(6分),
cos4x…(6分),∴周期T=
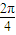 …(7分),
…(7分),最小值为:
 -
- =
= …(9分)
…(9分)由2kπ≤4x≤2kπ+π,(k∈Z)得:
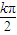 ≤x≤
≤x≤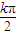 +
+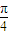 ,(k∈Z)
,(k∈Z)∴单调递减区间[
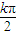 ,
,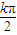 +
+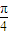 ],(k∈Z)…(12分) 注:丢掉k∈Z扣1分.
],(k∈Z)…(12分) 注:丢掉k∈Z扣1分.点评:本题考查二倍角的余弦,三角函数的平方关系式及三角函数的周期性及其求法,突出考查余弦函数的单调性,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 已知函数y=f(x)的图象如图所示,则不等式f(
已知函数y=f(x)的图象如图所示,则不等式f(