题目内容
（2013•和平区二模）在△ABC中，A=
，cosB=
．
（I）求cos C；
（II）设BC=
，求AC和AB．
| π |
| 4 |
| ||
| 10 |
（I）求cos C；
（II）设BC=
| 5 |
分析：（I）由cosB的值及B为三角形的内角，利用同角三角函数间的基本关系求出sinB的值，由三角形的内角和定理表示出C，再利用诱导公式及两角和与差的余弦函数公式即可求出cosC的值；
（II）由BC，sinA，sinB的值，利用正弦定理求出AC的长，再利用余弦定理即可求出AB的长．
（II）由BC，sinA，sinB的值，利用正弦定理求出AC的长，再利用余弦定理即可求出AB的长．
解答：解：（I）∵cosB=
，B∈（0，π），
∴sinB=
=
，
∵C=π-（A+B），A=
，
∴cosC=-cos（
+B）=-
×
+
×
=
；
（II）根据正弦定理
=
得：AC=
=
=3，
再根据余弦定理得：AB2=9+5-2×3×
×
=8，
则AB=2
．
| ||
| 10 |
∴sinB=
| 1-cos2B |
3
| ||
| 10 |
∵C=π-（A+B），A=
| π |
| 4 |
∴cosC=-cos（
| π |
| 4 |
| ||
| 2 |
| ||
| 10 |
| ||
| 2 |
3
| ||
| 10 |
| ||
| 5 |
（II）根据正弦定理
| AC |
| sinB |
| BC |
| sinA |
| BCsinB |
| sinA |
| ||||||
|
再根据余弦定理得：AB2=9+5-2×3×
| 5 |
| ||
| 5 |
则AB=2
| 2 |
点评：此题考查了正弦、余弦定理，诱导公式，以及同角三角函数间的基本关系，熟练掌握定理是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
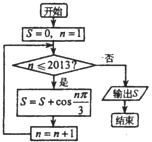（2013•和平区二模）阅读如图所示的程序框图，运行相应的程序，则输出的结果S的值为（ ）
（2013•和平区二模）已知函数y=Asin（ωx+φ）（A＞0，ω＞0），|φ|＜π）的部分图象如图所示，则它的解析式为（ ）