题目内容
已知函数 的定义域为M,集合N={y|y>1},则M∩N=
的定义域为M,集合N={y|y>1},则M∩N=
- A.[0,2)
- B.(0,2)
- C.(1,2]
- D.[1,2)
C
分析:根据负数没有平方根列出关于x的不等式,求出不等式的解集即为集合M,然后求出两集合的交集即可.
解答:由函数 有意义,得到2-x≥0,
有意义,得到2-x≥0,
解得:x≤2,所以集合M={x|x≤2};
又∵集合N={y|y>1},
∴M∩N=(1,2].
故选C
点评:此题属于以函数的定义域为平台,考查了交集的运算.此类题往往借助数轴来计算,会收到意想不到的收获.
分析:根据负数没有平方根列出关于x的不等式,求出不等式的解集即为集合M,然后求出两集合的交集即可.
解答:由函数
 有意义,得到2-x≥0,
有意义,得到2-x≥0,解得:x≤2,所以集合M={x|x≤2};
又∵集合N={y|y>1},
∴M∩N=(1,2].
故选C
点评:此题属于以函数的定义域为平台,考查了交集的运算.此类题往往借助数轴来计算,会收到意想不到的收获.

练习册系列答案
相关题目
 的定义域为M.
的定义域为M. 的定义域为M.
的定义域为M. 的定义域为M,函数
的定义域为M,函数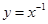 的定义域为N,则
的定义域为N,则 ( )
( ) 且
且 B.
B.  且
且 D.
D.

 的定义域为M,函数
的定义域为M,函数 的定义域为N,则
的定义域为N,则 的定义域为M,g(x)=
的定义域为M,g(x)= 的定义域为N,则M∩N=
的定义域为N,则M∩N= (B)
(B) (C)
(C) (D)
(D)