题目内容
11.如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F,点A,B在椭圆E上,直线AB经过坐标原点O.若AF⊥x轴,cos∠AFB=-$\frac{3}{5}$,则椭圆E的离心率e=$\frac{1}{2}$.分析 通过设A(c,y)并代入椭圆方程可知|AF|=$\frac{{b}^{2}}{a}$,通过连结点B与椭圆左焦点F′,利用椭圆定义可知|BF|=2a-|BF′|=2a-$\frac{{b}^{2}}{a}$,利用cos∠AFB=-$\frac{3}{5}$可知$\frac{|BF′|}{|BF|}$=$\frac{3}{5}$,进而计算可得结论.
解答 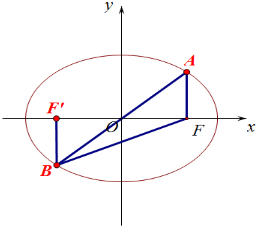 解:根据题意可知F(c,0),
解:根据题意可知F(c,0),
如图设A(c,y),则$\frac{{c}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
∴$\frac{{y}^{2}}{{b}^{2}}$=1-$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$,
∴y=±$\frac{{b}^{2}}{a}$,即|AF|=$\frac{{b}^{2}}{a}$,
连结点B与椭圆左焦点F′,
由题可知BF′⊥x轴,且|BF′|=|AF|=$\frac{{b}^{2}}{a}$,
∴|BF|=2a-|BF′|=2a-$\frac{{b}^{2}}{a}$,
∵cos∠AFB=-$\frac{3}{5}$,
∴cos∠FBF′=$\frac{3}{5}$,即$\frac{|BF′|}{|BF|}$=$\frac{3}{5}$,
∴$\frac{\frac{{b}^{2}}{a}}{2a-\frac{{b}^{2}}{a}}$=$\frac{3}{5}$,整理得:$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$,
∴离心率e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{3}{4}}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查椭圆的离心率,注意解题方法的积累,属于中档题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 1 | B. | -1 | C. | ±1 | D. | 不存在 |
| A. | 64 | B. | 81 | C. | 243 | D. | 128 |
| A. | -2 | B. | $-\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
| A. | 非负数 | B. | 正数 | C. | 负数 | D. | 整数 |