题目内容
已知函数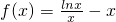 .
.
(Ⅰ)求函数f(x)的最大值;
(Ⅱ)设m>0,求f(x)在[m,2m]上的最大值;
(III)试证明:对?n∈N*,不等式 恒成立.
恒成立.
解:(Ⅰ)∵函数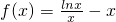 ,∴
,∴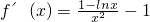 ,令f′(x)=0,得x2=1-lnx,显然x=1是此方程的解;
,令f′(x)=0,得x2=1-lnx,显然x=1是此方程的解;
令g(x)=x2+lnx-1,其中x∈(0,+∞),则 ;
;
∴函数g(x)在(0,+∞)上单调递增,又x=1是方程f′(x)=0的唯一解,
∴当x=1时,函数有最大值f(x)max=f(1)=-1.
(Ⅱ)由(Ⅰ)知,函数f(x)在区间(0,1)上单调递增,在(1,+∞)上单调递减;
故①当0<2m≤1,即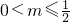 时,f(x)在[m,2m]上单调递增,
时,f(x)在[m,2m]上单调递增, ;
;
②当m≥1时,f(x)在[m,2m]上单调递减, ;
;
③当m<1<2m,即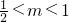 时,f(x)max=f(1)=-1.
时,f(x)max=f(1)=-1.
(Ⅲ)由(Ⅰ)知,x∈(0,+∞)时,f(x)max=f(1)=-1,
∴在(0,+∞)上恒有 ,当且仅当x=1时“=”成立,
,当且仅当x=1时“=”成立,
∴对任意的x∈(0,+∞)恒有lnx≤x(x-1);
∵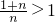 ,∴
,∴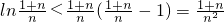 ,
,
即对?n∈N*,不等式 恒成立.
恒成立.
分析:(Ⅰ)由函数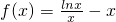 ,得f′(x),令f′(x)=0,得此方程的解;从而求得函数f(x)的最大值.
,得f′(x),令f′(x)=0,得此方程的解;从而求得函数f(x)的最大值.
(Ⅱ)由(Ⅰ)知,函数f(x)在区间(0,1)上单调递增,在(1,+∞)上单调递减;
故①当0<2m≤1,即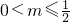 时,f(x)在[m,2m]上单调递增,最大值是f(2m);
时,f(x)在[m,2m]上单调递增,最大值是f(2m);
②当m≥1时,f(x)在[m,2m]上单调递减,最大值是f(m);
③当m<1<2m,即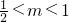 时,最大值是f(1).
时,最大值是f(1).
(Ⅲ)由(Ⅰ)知,x∈(0,+∞)时,f(x)max=f(1)=-1,即在(0,+∞)上,恒有 ,当且仅当x=1时“=”成立,即是恒有lnx≤x(x-1);由于
,当且仅当x=1时“=”成立,即是恒有lnx≤x(x-1);由于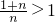 ,∴
,∴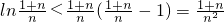 ,即证.
,即证.
点评:本题综合考查了利用导数研究函数的单调区间以及根据函数的增减性求得函数的最值问题,也考查了利用函数证明不等式恒成立的问题,属于较难的题目.
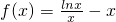 ,∴
,∴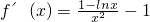 ,令f′(x)=0,得x2=1-lnx,显然x=1是此方程的解;
,令f′(x)=0,得x2=1-lnx,显然x=1是此方程的解;令g(x)=x2+lnx-1,其中x∈(0,+∞),则
 ;
;∴函数g(x)在(0,+∞)上单调递增,又x=1是方程f′(x)=0的唯一解,
∴当x=1时,函数有最大值f(x)max=f(1)=-1.
(Ⅱ)由(Ⅰ)知,函数f(x)在区间(0,1)上单调递增,在(1,+∞)上单调递减;
故①当0<2m≤1,即
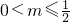 时,f(x)在[m,2m]上单调递增,
时,f(x)在[m,2m]上单调递增, ;
;②当m≥1时,f(x)在[m,2m]上单调递减,
 ;
;③当m<1<2m,即
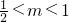 时,f(x)max=f(1)=-1.
时,f(x)max=f(1)=-1.(Ⅲ)由(Ⅰ)知,x∈(0,+∞)时,f(x)max=f(1)=-1,
∴在(0,+∞)上恒有
 ,当且仅当x=1时“=”成立,
,当且仅当x=1时“=”成立,∴对任意的x∈(0,+∞)恒有lnx≤x(x-1);
∵
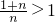 ,∴
,∴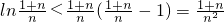 ,
,即对?n∈N*,不等式
 恒成立.
恒成立.分析:(Ⅰ)由函数
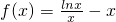 ,得f′(x),令f′(x)=0,得此方程的解;从而求得函数f(x)的最大值.
,得f′(x),令f′(x)=0,得此方程的解;从而求得函数f(x)的最大值.(Ⅱ)由(Ⅰ)知,函数f(x)在区间(0,1)上单调递增,在(1,+∞)上单调递减;
故①当0<2m≤1,即
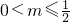 时,f(x)在[m,2m]上单调递增,最大值是f(2m);
时,f(x)在[m,2m]上单调递增,最大值是f(2m);②当m≥1时,f(x)在[m,2m]上单调递减,最大值是f(m);
③当m<1<2m,即
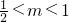 时,最大值是f(1).
时,最大值是f(1).(Ⅲ)由(Ⅰ)知,x∈(0,+∞)时,f(x)max=f(1)=-1,即在(0,+∞)上,恒有
 ,当且仅当x=1时“=”成立,即是恒有lnx≤x(x-1);由于
,当且仅当x=1时“=”成立,即是恒有lnx≤x(x-1);由于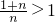 ,∴
,∴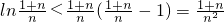 ,即证.
,即证.点评:本题综合考查了利用导数研究函数的单调区间以及根据函数的增减性求得函数的最值问题,也考查了利用函数证明不等式恒成立的问题,属于较难的题目.

练习册系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数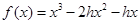 ,若
,若 且
且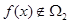 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得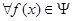 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


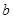
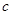




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.