题目内容
如下图,B地在A地的正东方向4 km处,C地在B地的北偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、C两地修建公路的费用都是a万元/km,那么修建这两条公路的总费用最低是( )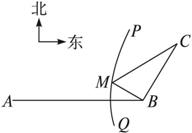
A.(![]() +1)a万元 B.(2
+1)a万元 B.(2![]() -2)a万元
-2)a万元
C.2![]() a万元 D.(
a万元 D.(![]() -1)a万元
-1)a万元
答案:B设总费用为y万元,则y=a·(MB+MC).
∵河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km,∴曲线PQ是双曲线的一支,B为焦点,且a=1,c=2.由双曲线的第一定义,得MA-MB=2a,即MB=MA-2.
∴y=a·(MA+MC-2)≥a·(AC-2).以直线AB为x轴,中点为坐标原点建立直角坐标系,则A(-2,0),C(3,![]() ).∴AC=
).∴AC=![]() =2
=2![]() .故y≥(2
.故y≥(2![]() -2)a(万元).
-2)a(万元).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


