题目内容
在△ABC中,cosA=-
,cosB=
,BC=5,△ABC的面积=
.
| 5 |
| 13 |
| 3 |
| 5 |
| 8 |
| 3 |
| 8 |
| 3 |
分析:由cosA与cosB的值,利用同角三角函数间的基本关系求出sinA与sinB的值,由诱导公式得到sinC=sin(A+B),利用两角和与差的正弦函数公式化简后,将各自的值代入求出sinC的值,再由BC,即a的值,利用正弦定理求出c的值,再由a,c及cosB的值,利用三角形的面积公式即可求出三角形的ABC面积.
解答:解:∵cosA=-
,cosB=
,
∴sinA=
=
,sinB=
=
,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=
×
-
×
=
,
∵BC=a=5,
∴由正弦定理
=
得:c=
=
,
则S△ABC=
acsinB=
×5×
×
=
.
故答案为:
| 5 |
| 13 |
| 3 |
| 5 |
∴sinA=
| 1-cos2A |
| 12 |
| 13 |
| 1-cos2B |
| 4 |
| 5 |
∴sinC=sin(A+B)=sinAcosB+cosAsinB=
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
| 16 |
| 65 |
∵BC=a=5,
∴由正弦定理
| a |
| sinA |
| c |
| sinC |
| asinC |
| sinA |
| 4 |
| 3 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 5 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:此题属于解三角形的题型,涉及的知识有:正弦定理,同角三角函数间的基本关系,三角形的面积公式,以及两角和与差的正弦函数公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
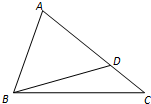 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=