题目内容
已知在三棱锥S-ABC中,∠ACB=90°,又SA⊥平面ABC,AD⊥SC于D,求证:AD⊥平面SBC。

证明:易证SA⊥面ABC,∴BC ⊥SA,
又BC⊥AC,且AC、SA是面SAC内的两相交线,
∴BC⊥面SAC,
又AD 面SAC,
面SAC,
∴BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,
∴AD⊥面SBC。
又BC⊥AC,且AC、SA是面SAC内的两相交线,
∴BC⊥面SAC,
又AD
 面SAC,
面SAC,∴BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,
∴AD⊥面SBC。

练习册系列答案
相关题目
 :
: :
: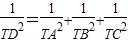 ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积)