题目内容
(08年鹰潭市一模理)(14分)已知函数![]() 满足
满足![]() ,
,![]() ,
,![]() ;且使
;且使![]() 成立的实数
成立的实数![]() 只有一个。
只有一个。
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,证明数列
,证明数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,如果![]() ,
,
![]() ,证明:
,证明:![]() ,
,![]() 。
。
解析:(Ⅰ)由![]() ,
,![]() ,
,![]() ,得
,得![]() .…1分
.…1分
由![]() ,得
,得![]() .…………2分
.…………2分
由![]() 只有一解,即
只有一解,即![]() ,也就是
,也就是![]() 只有一解,
只有一解,
∴![]() ∴
∴![]() .…………3分
.…………3分
∴![]() .故
.故![]() .…………………4分
.…………………4分
(Ⅱ)解法一:∵![]() ,
,![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,……………5分
,……………5分
猜想,![]() .……………6分
.……………6分
下面用数学归纳法证明:
10 当n=1时,左边=![]() ,右边=
,右边=![]() ,∴命题成立. ……………7分
,∴命题成立. ……………7分
20 假设n=k时,命题成立,即![]() ;当 n=k+1时,
;当 n=k+1时,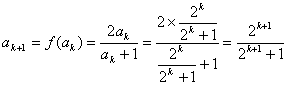 ,
,
∴当 n=k+1时,命题成立. ………………8分
由10,20可得,当![]() 时,有
时,有![]() .……………9分
.……………9分
∵![]() ,∴
,∴![]()
∴![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,其通项公式为
的等比数列,其通项公式为![]() .………10分
.………10分
解法二:∵![]() ,
,![]() ∴
∴![]() ………5分
………5分
即![]() ,………8分
,………8分
∴![]() ………9分
………9分
![]() ,
,![]() ………10分
………10分
(Ⅲ)当![]() 为偶数时,
为偶数时,
![]()
即![]() ………………12分
………………12分
∴![]()
即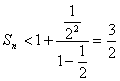 .…………………14分
.…………………14分

练习册系列答案
相关题目
