Question

（本小题满分12分）

如图，在四棱锥中，平面，底面为直角梯形，∥，

，

（Ⅰ）求异面直线与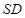所成角的大小；

（Ⅱ）求证：⊥平面；

（Ⅲ）求直线与平面所成角大小的正切值.

 

 

 

 

 

Answer 1

【答案】

（Ⅰ）解：∵∥

异面直线与所成角是∠SDA或其补角

∵平面，平面

在Rt△SAD中, ∵,∠SDA=45^o

异面直线与所成角的大小为45^o.

（Ⅱ）证明：

又∵ 

（Ⅲ）由（Ⅱ）得，是在平面上的射影，

∠CSB是与底面所成角

在Rt△CSB中

tan∠CSB=

与底面所成角的正切值为

 

【解析】略