题目内容
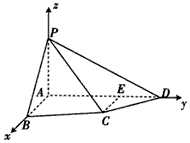
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD中,AB⊥AD,AB+AD=4,CD=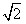 ,∠CDA=45°,
,∠CDA=45°,
(Ⅰ)求证:平面PAB⊥平面PAD;
(Ⅱ)设AB=AP,
(ⅰ)若直线PB与平面PCD所成的角为30°,求线段AB的长;
(ⅱ)在线段AD上是否存在一个点G,使得点G到点P,B,C,D的距离都相等?说明理由.
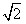 ,∠CDA=45°,
,∠CDA=45°,(Ⅰ)求证:平面PAB⊥平面PAD;
(Ⅱ)设AB=AP,
(ⅰ)若直线PB与平面PCD所成的角为30°,求线段AB的长;
(ⅱ)在线段AD上是否存在一个点G,使得点G到点P,B,C,D的距离都相等?说明理由.
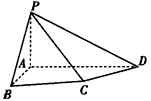
(Ⅰ)证明:因为PA⊥平面ABCD,AB 平面ABCD, 平面ABCD,所以PA⊥AB, 又AB⊥AD,PA∩AD=A, 所以AB⊥平面PAD, 又AB 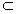 平面PAB, 平面PAB,所以平面PAB⊥平面PAD。 |
 |
| (Ⅱ)解:以A为坐标原点,建立空间直角坐标系A-xyz(如图), 在平面ABCD内,作CE∥AB交AD于点E,则CE⊥AD, 在Rt△CDE中,DE=CD·cos45°=1,CE=CD·sin45°=1, 设AB=AP=t,则B(t,0,0),P(0,0,t), 由AB+AD=4得AD=4-t, 所以E(0,3-t,0),C(1,3-t,0),D(0,4-t,0), 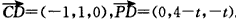 , ,(i)设平面PCD的法向量为n=(x,y,z), 由 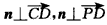 ,得 ,得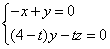 , ,取x=t,得平面PCD的一个法向量n=(t,t,4-t), 又 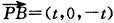 , ,故由直线PB与平面PCD所成的角为30°得 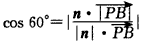 , ,即 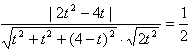 ,解得 ,解得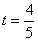 或t=4(舍去,因为 或t=4(舍去,因为AD=4-t>0), 所以 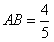 。 。(ii)假设在线段AD上存在一点G,使得点G到点P,B,C,D的距离都相等. 设G(0,m,0)(其中0≤m≤4-t), 则 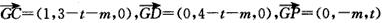 , ,由 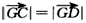 得12+(3-t-m)2=(4-t-m)2,即t=3-m;(1) 得12+(3-t-m)2=(4-t-m)2,即t=3-m;(1)由 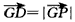 得(4-t-m)2=m2+t2, (2) 得(4-t-m)2=m2+t2, (2) 由(1)、(2)消去t,化简得m2-3m+4=0, (3) 由于方程(3)没有实数根,所以在线段AD上不存在一个点G, 使得点G到点P,C,D的距离都相等. 从而,在线段AD上不存在一个点G, 使得点G到点P,B,C,D的距离都相等. |
 |

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=