题目内容
下列命题中,真命题是( )
A、?x∈R,sin2
| ||||||
| B、?x∈(0,π),sinx>cosx | ||||||
| C、?x∈R,x2+x=-1 | ||||||
| D、?x∈(0,+∞),ex>1+x |
分析:根据同角三角函数的平方关系,我们可以判断A的正误;
正弦函数和余弦函数的图象与性质,我们可以判断B的真假;
解一元二次不等式,可以判断C的正误;
根据指数函数y=ex和y=1+x图象特征,我们可判断D的对错,进而得到答案.
正弦函数和余弦函数的图象与性质,我们可以判断B的真假;
解一元二次不等式,可以判断C的正误;
根据指数函数y=ex和y=1+x图象特征,我们可判断D的对错,进而得到答案.
解答:解:对于A,由同角三角函数和平方关系,我们知道?x∈R,sin2
+cos2
=1,所以A为假命题;
对于B,取特殊值:当时x=
时,sinx=cosx=
,所以B为假命题;
对于C,一元二次方程根的判别式△=1-4=-3<0,所以原方程没有实数根,所以C为假命题;
对于D,构造函数y=ex-x,x∈(0,+∞)
求出导数:y/=ex-1,可得当时y/<0,函数为减函数,
当x∈(1,+∞)时y/>0,函数为增函数,
所以当x=1时函数的最小值为e-1,即?x∈(0,+∞),ex-x≥e-1>1,
移项,得ex>1+x,因此“?x∈(0,+∞),ex>1+x”是真命题
故选D
| x |
| 2 |
| x |
| 2 |
对于B,取特殊值:当时x=
| π |
| 4 |
| ||
| 2 |
对于C,一元二次方程根的判别式△=1-4=-3<0,所以原方程没有实数根,所以C为假命题;
对于D,构造函数y=ex-x,x∈(0,+∞)
求出导数:y/=ex-1,可得当时y/<0,函数为减函数,
当x∈(1,+∞)时y/>0,函数为增函数,
所以当x=1时函数的最小值为e-1,即?x∈(0,+∞),ex-x≥e-1>1,
移项,得ex>1+x,因此“?x∈(0,+∞),ex>1+x”是真命题
故选D
点评:本题考查的知识点是命题的真假判断与应用,其中利用函数的性质,逐一分析四个结论的正误是解答本题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
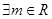 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1