题目内容
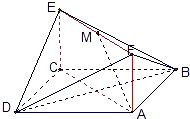
 如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.
如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.
(1)证明:ME∥平面FAD;
(2)试探究点M的位置,使平面AME⊥平面AEF.
解:(1)∵FD⊥平面ABCD,EB⊥平面ABCD,∴FD∥EB,又 AD∥BC且AD∩FD=D,BC∩BE=B,
∴平面FAD∥平面EBC,ME?平面EBC,∴ME∥平面FAD.
(2)以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,
依题意,得D(0,0,0),A(1,0,0),F(0,0,1),C(0,1,0),B(1,1,0),E(1,1,1),
设M(λ,1,0),平面AEF的法向量为 =(x1,y1,z1),平面AME的法向量为
=(x1,y1,z1),平面AME的法向量为 =(x2,y2,z2),
=(x2,y2,z2),
∵ =(0,1,1),
=(0,1,1), =(-1,0,1),∴
=(-1,0,1),∴ ,∴
,∴ .
.
取z1=1,得x1=1,y1=-1,∴ =(1,-1,0). 又
=(1,-1,0). 又 =(λ-1,1,0),
=(λ-1,1,0), =(0,1,1),
=(0,1,1),
∴ ,∴
,∴ ,取x2=1得y2=1-λ,z2=λ-1,∴
,取x2=1得y2=1-λ,z2=λ-1,∴ =(1,1-λ,λ-1),
=(1,1-λ,λ-1),
若平面AME⊥平面AEF,则 ⊥
⊥ ,∴
,∴
 =0,∴1-(1-λ)+(λ-1)=0,解得λ=
=0,∴1-(1-λ)+(λ-1)=0,解得λ= ,
,
此时M为BC的中点.所以当M在BC的中点时,AME⊥平面AEF.
分析:(1)由FD∥EB,AD∥BC,证明平面FAD∥平面EBC,从而证明 ME∥平面FAD.
(2)建立空间直角坐标D-xyz,设M(λ,1,0),求出平面AEF的法向量为 的坐标,平面AME的法向量为
的坐标,平面AME的法向量为 的坐标,由
的坐标,由
 =0,可得λ值,从而确定M在线段BC上的位置.
=0,可得λ值,从而确定M在线段BC上的位置.
点评:本题考查证明先面平行的方法,以及利用两个平面的法向量垂直来证明两个平面垂直,求出两个平面的法向量是解题的
关键.
∴平面FAD∥平面EBC,ME?平面EBC,∴ME∥平面FAD.
(2)以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,
依题意,得D(0,0,0),A(1,0,0),F(0,0,1),C(0,1,0),B(1,1,0),E(1,1,1),
设M(λ,1,0),平面AEF的法向量为
 =(x1,y1,z1),平面AME的法向量为
=(x1,y1,z1),平面AME的法向量为 =(x2,y2,z2),
=(x2,y2,z2),∵
 =(0,1,1),
=(0,1,1), =(-1,0,1),∴
=(-1,0,1),∴ ,∴
,∴ .
.取z1=1,得x1=1,y1=-1,∴
 =(1,-1,0). 又
=(1,-1,0). 又 =(λ-1,1,0),
=(λ-1,1,0), =(0,1,1),
=(0,1,1),∴
 ,∴
,∴ ,取x2=1得y2=1-λ,z2=λ-1,∴
,取x2=1得y2=1-λ,z2=λ-1,∴ =(1,1-λ,λ-1),
=(1,1-λ,λ-1),若平面AME⊥平面AEF,则
 ⊥
⊥ ,∴
,∴
 =0,∴1-(1-λ)+(λ-1)=0,解得λ=
=0,∴1-(1-λ)+(λ-1)=0,解得λ= ,
,此时M为BC的中点.所以当M在BC的中点时,AME⊥平面AEF.
分析:(1)由FD∥EB,AD∥BC,证明平面FAD∥平面EBC,从而证明 ME∥平面FAD.
(2)建立空间直角坐标D-xyz,设M(λ,1,0),求出平面AEF的法向量为
 的坐标,平面AME的法向量为
的坐标,平面AME的法向量为 的坐标,由
的坐标,由
 =0,可得λ值,从而确定M在线段BC上的位置.
=0,可得λ值,从而确定M在线段BC上的位置.点评:本题考查证明先面平行的方法,以及利用两个平面的法向量垂直来证明两个平面垂直,求出两个平面的法向量是解题的
关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.