题目内容
(2012•孝感模拟)已知f(x)=(2
cos
+2sin
)cos
.
(I)求f(
)的值;
(II)在△ABC中,角A,B,C所对的边分别为a,b,c若f(c)=
+1,且b2=ac,求sinA的值.
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
(I)求f(
| 17π |
| 12 |
(II)在△ABC中,角A,B,C所对的边分别为a,b,c若f(c)=
| 3 |
分析:(I)利用多项式乘以单项式的法则将函数解析式化简,再利用二倍角的正弦、余弦函数公式化简,然后利用两角和与差的余弦函数公式及特殊角的三角函数值化为一个角的余弦函数,将x=
代入化简后的式子中计算,即可得到所求的函数值;
(II)由第一问求出的函数解析式及f(C)=
+1,求出cos(C-
)的值,由C为三角形的内角,利用特殊角的三角函数值求出C为直角,得到三角形ABC为直角三角形,利用勾股定理得到c2=a2+b2,再将b2=ac代入,整理后得到关于
的芙蓉城,求出方程的解得到
的值,利用锐角三角函数定义即可求出sinA的值.
| 17π |
| 12 |
(II)由第一问求出的函数解析式及f(C)=
| 3 |
| π |
| 6 |
| a |
| c |
| a |
| c |
解答:解:(I)f(x)=(2
cos
+2sin
)cos
=2
cos2
+2sin
cos
=
(1+cosx)+sinx
=
cosx+sinx+
=2cos(x-
)+
,
则f(
)=2cos(
-
)+
=2cos
+
=
-
;
(II)∵f(C)=
+1,
∴2cos(C-
)+
=
+1,即cos(C-
)=
,
又C为三角形的内角,
∴C=
,又b2=ac,
在Rt△ABC中,根据勾股定理得:c2=a2+b2=a2+ac,
∴(
)2+
-1=0,
解得:
=
,
∵0<sinA<1,
∴sinA=
=
.
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=2
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=
| 3 |
=
| 3 |
| 3 |
=2cos(x-
| π |
| 6 |
| 3 |
则f(
| 17π |
| 12 |
| 17π |
| 12 |
| π |
| 6 |
| 3 |
| 5π |
| 4 |
| 3 |
| 3 |
| 2 |
(II)∵f(C)=
| 3 |
∴2cos(C-
| π |
| 6 |
| 3 |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
又C为三角形的内角,
∴C=
| π |
| 2 |
在Rt△ABC中,根据勾股定理得:c2=a2+b2=a2+ac,
∴(
| a |
| c |
| a |
| c |
解得:
| a |
| c |
-1±
| ||
| 2 |
∵0<sinA<1,
∴sinA=
| a |
| c |
| ||
| 2 |
点评:此题属于解三角形的题型,涉及的知识有:二倍角的正弦、余弦函数公式,两角和与差的余弦函数公式,勾股定理,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
(2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )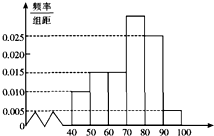 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: