题目内容
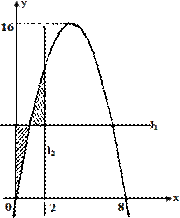 已知二次函数
已知二次函数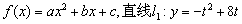 (其中
(其中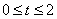 ,t为常数),
,t为常数),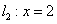 的图象如图所示.
的图象如图所示.
(1)根据图象求a、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若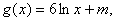 问是否存在实数m, 使得
问是否存在实数m, 使得
 的图象与
的图象与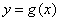 的图象有且只有三个不同的
的图象有且只有三个不同的
交点?若存在,求出m的值;若不存在,说明理由.
解:(1)由图形知:
解之,得
∴函数f(x)的解析式为
(2)由 得
得 

∵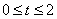 ,∴
,∴
∴直线l1与f(x)的图象的交点坐标为
由定积分的几何意义知:


 .
.
(3)令
因为x>0,要使函数 与函数
与函数 有且仅有2个不同的交点,则函数
有且仅有2个不同的交点,则函数
 的图象与x轴的正半轴有且只有两个不同的交点.
的图象与x轴的正半轴有且只有两个不同的交点.
 .
.
当x∈(0,1)时, 是增函数;
是增函数;
当x∈(1,3)时, 是减函数;
是减函数;
当x∈(3,+∞)时, 是增函数;
是增函数;
当x=1或x=3时, .
.
∴
 .
.
又因为当x无限趋近于零时,
当x无限大时,
所以要使 有且仅有三个不同的正根,必须且只须
有且仅有三个不同的正根,必须且只须
 ,即
,即
故
∴ 时,函数
时,函数 与
与 的图象有且只有三个不同交点
的图象有且只有三个不同交点

练习册系列答案
相关题目
 ,
, ,
, ,
, ,
, ,…,则
,…,则
 为
为
 都成立,则
都成立,则  B.
B.
 D.
D. 和
和 的大小关系不确定
的大小关系不确定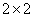 列联表:
列联表: 
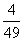 .
.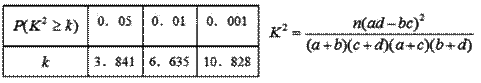 附:
附: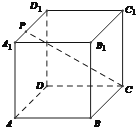
 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则 的值是 ( )
的值是 ( )  B.
B. C.
C.  D.
D.

 满足约束条件
满足约束条件 ,则
,则 的最大值为 ( )
的最大值为 ( )