题目内容
已知集合MD是满足下列性质函数f(x)的全体:若函数f(x)的定义域为D,对任意的x1,x2∈D,(x1≠x2)有|f(x1)-f(x2)|<|x1-x2|.(1)当D=(0,+∞)时,f(x)=lnx是否属于MD,若属于MD,给予证明,否则说明理由;
(2)当D=(0,![]() ),函数f(x)=x3+ax+b时,若 f(x)∈M.求实数a的取值范围.?
),函数f(x)=x3+ax+b时,若 f(x)∈M.求实数a的取值范围.?
分析:本题若用常规解法,解答较繁;若用导数的几何意义,则十分简单.
解:(1)∵f′(x)=![]() ,∴若x∈(0,1),f′(x)>1
,∴若x∈(0,1),f′(x)>1![]() |f′(x)|>1,
|f′(x)|>1,
∴|![]() |>1.
|>1.
当x1,x2∈(0,1)时,f(x)=lnxMD.
(2)由f(x)=x3+ax+b![]() f′(x)=3x2+a,
f′(x)=3x2+a,
当x∈(0,![]() )时,a<f′(x)<1+a.
)时,a<f′(x)<1+a.
∵f(x)∈MD,
∴|f(x1)-f(x2)|<|x1-x2|,即|![]() |<1.
|<1.
∴![]()
![]() -1≤a≤0为所求.
-1≤a≤0为所求.

练习册系列答案
相关题目
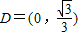 ,函数f(x)=x3+ax+b时,若f(x)∈MD,求实数a的取值范围.
,函数f(x)=x3+ax+b时,若f(x)∈MD,求实数a的取值范围.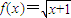 属于MD,求k的取值范围;
属于MD,求k的取值范围;