题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,在
,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)中求的是在x=1的切线方程,所以直接出函数在x=1的导数,和切点即可解决。(2)求单调性区间,先注意定义域,再求导数等于0的根,一般对于含参的问题,我们先看是否能因式分解。(3)存在![]() 成立,先变形为
成立,先变形为![]() ,从而构造函数
,从而构造函数![]() 在
在![]() 上的最小值
上的最小值![]() .同时注意第(2)问己求对本问的应用。
.同时注意第(2)问己求对本问的应用。
试题解析:
(1)当![]() 时,
时, ![]() ,切点
,切点![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() .
.
(2)![]() ,定义域为
,定义域为![]() ,
,
![]() ,
,
①当![]() ,即
,即![]() 时,令
时,令![]() ,因为
,因为![]() ,所以
,所以![]() .
.
令![]() ,因为
,因为![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() ,令
,令![]() 恒成立,
恒成立,
综上,当![]() 时,
时, ![]() 唉
唉![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
(3)由题意可知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
即在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,
即函数![]() 在
在![]() 上的最小值
上的最小值![]() .
.
由第(2)问,
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ;
;
③当![]() ,即
,即![]() 时,
时, ![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
此时不存在![]() 使得
使得![]() 成立.
成立.

练习册系列答案
相关题目
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
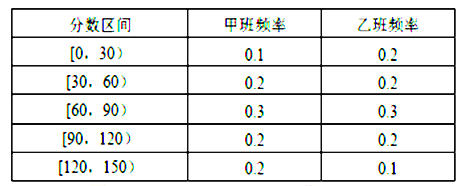
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
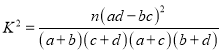 ,其中
,其中![]() .
.