题目内容
边长为a的正三角形内任一点到三边距离之和为定值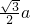 ,类比到空间,棱长均为a的三棱锥内任一点到各面距离之和为
,类比到空间,棱长均为a的三棱锥内任一点到各面距离之和为
- A.

- B.
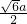
- C.
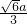
- D.

C
分析:用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,画出图形,利用正四面体的一个面上的直角三角形勾股定理做出结果,用这个结果乘以4得到距离距离之和.
解答: 解:本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,
解:本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,
如图:
由棱长为a可以得到BF= ,BO=AO=
,BO=AO= ,
,
在直角三角形中,根据勾股定理可以得到
BO2=BE2+OE2,
把数据代入得到OE=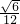 ,
,
∴棱长为a的三棱锥内任一点到各个面的距离之和4×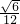 =
=
故选C.
点评:本题考查类比推理,考查利用特殊的图形解决一般的问题,解题的关键是在正四面体中的勾股定理和正三角形的有关性质的应用,注意运算中不要出现失误.
分析:用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,画出图形,利用正四面体的一个面上的直角三角形勾股定理做出结果,用这个结果乘以4得到距离距离之和.
解答:
 解:本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,
解:本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,如图:
由棱长为a可以得到BF=
 ,BO=AO=
,BO=AO= ,
,在直角三角形中,根据勾股定理可以得到
BO2=BE2+OE2,
把数据代入得到OE=
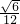 ,
,∴棱长为a的三棱锥内任一点到各个面的距离之和4×
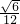 =
=
故选C.
点评:本题考查类比推理,考查利用特殊的图形解决一般的问题,解题的关键是在正四面体中的勾股定理和正三角形的有关性质的应用,注意运算中不要出现失误.

练习册系列答案
相关题目
边长为a的正三角形内任一点到三边距离之和为定值
a,类比到空间,棱长均为a的三棱锥内任一点到各面距离之和为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
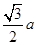 ,类比上述结论,在边长为a的正四面体内任一点到其四个面的距离之和为定值 。
,类比上述结论,在边长为a的正四面体内任一点到其四个面的距离之和为定值 。