题目内容
函数y=f (x )=-x3+ax2+b(a,b∈R ),
(Ⅰ)要使y=f(x)在(0,1)上单调递增,求a的取值范围;
(Ⅱ)当a>0时,若函数满足y极小值=1,y极大值=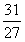 ,求函数y=f(x)的解析式;
,求函数y=f(x)的解析式;
(Ⅲ)若x∈[0,1]时,y=f(x)图象上任意一点处的切线倾斜角为θ,求当0≤θ≤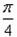 时a的取值范围。
时a的取值范围。
(Ⅰ)要使y=f(x)在(0,1)上单调递增,求a的取值范围;
(Ⅱ)当a>0时,若函数满足y极小值=1,y极大值=
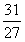 ,求函数y=f(x)的解析式;
,求函数y=f(x)的解析式;(Ⅲ)若x∈[0,1]时,y=f(x)图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
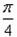 时a的取值范围。
时a的取值范围。解:(Ⅰ)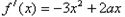 ,
,
要使f(x)在(0,1)上单调递增,
则x∈(0,1)时,f′(x)≥0恒成立,
∴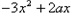 ≥0,
≥0,
即当x∈(0,1)时,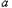 ≥
≥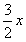 恒成立,
恒成立,
∴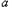 ≥
≥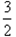 ,即a的取值范围是[
,即a的取值范围是[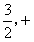 ∞
∞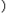 。
。
(Ⅱ)由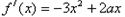 ,令f′(x)=0,得x=0或
,令f′(x)=0,得x=0或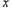 =
=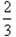
 ,
,
∵a>0,∴当x变化时,f′(x)、f(x)的变化情况如下表:
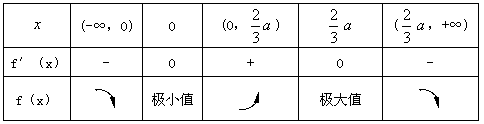
∴y极小值=f(0)=b=1,y极大值= =
=
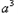 +
+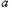 ·
·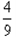
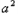 +1=
+1=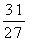 ,
,
∴b=1,a=1,
故f(x)=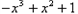 。
。
(Ⅲ)当x∈[0,1]时,tanθ=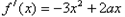 ,
,
由θ∈[0,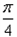 ],得0≤f′(x)≤1,
],得0≤f′(x)≤1,
即x∈[0,1]时,0≤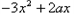 ≤1恒成立,
≤1恒成立,
当x=0时,a∈R,
当x∈(0,1]时,由 ≥0恒成立,
≥0恒成立,
由(Ⅰ)知 ≥
≥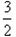 ,
,
由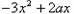 ≤1恒成立,a≤
≤1恒成立,a≤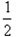 (3x+
(3x+ ),
),
∴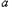 ≤
≤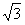 (等号在
(等号在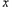 =
=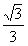 时取得);
时取得);
综上, ≤
≤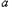 ≤
≤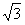 。
。
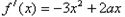 ,
,要使f(x)在(0,1)上单调递增,
则x∈(0,1)时,f′(x)≥0恒成立,
∴
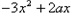 ≥0,
≥0,即当x∈(0,1)时,
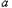 ≥
≥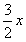 恒成立,
恒成立,∴
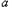 ≥
≥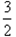 ,即a的取值范围是[
,即a的取值范围是[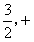 ∞
∞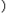 。
。(Ⅱ)由
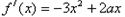 ,令f′(x)=0,得x=0或
,令f′(x)=0,得x=0或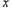 =
=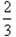
 ,
,∵a>0,∴当x变化时,f′(x)、f(x)的变化情况如下表:

∴y极小值=f(0)=b=1,y极大值=
 =
=
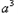 +
+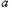 ·
·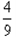
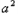 +1=
+1=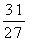 ,
,∴b=1,a=1,
故f(x)=
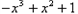 。
。(Ⅲ)当x∈[0,1]时,tanθ=
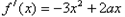 ,
,由θ∈[0,
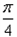 ],得0≤f′(x)≤1,
],得0≤f′(x)≤1,即x∈[0,1]时,0≤
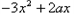 ≤1恒成立,
≤1恒成立,当x=0时,a∈R,
当x∈(0,1]时,由
 ≥0恒成立,
≥0恒成立,由(Ⅰ)知
 ≥
≥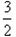 ,
,由
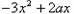 ≤1恒成立,a≤
≤1恒成立,a≤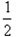 (3x+
(3x+ ),
),∴
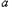 ≤
≤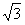 (等号在
(等号在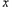 =
=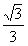 时取得);
时取得);综上,
 ≤
≤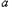 ≤
≤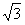 。
。
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 6、如图,函数y=f(x)的图象在点P处的切线方程,y=-x+5,则f(3)-f′(3)=
6、如图,函数y=f(x)的图象在点P处的切线方程,y=-x+5,则f(3)-f′(3)=