题目内容
已知函数f(x)=elnx+ (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数)
(I)若f(x)在x=x0处取得极值,且x0是f(x)的一个零点,求k的值;
(II)若k∈[1,e],求f(x)在区间[ ,1]上的最大值;
,1]上的最大值;
(III)设函数g(x)=f(x)-kx在区间( ,e)上是减函数,求k的取值范围.
,e)上是减函数,求k的取值范围.
解:(I)由已知f'(x0)=0,即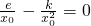 ,(2分)
,(2分)
∴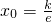 ,又f(x0)=0,即
,又f(x0)=0,即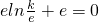 ,∴k=1.(4分)
,∴k=1.(4分)
(II)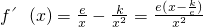 ,
,
∵1≤k≤e,∴ ,(6分)
,(6分)
由此得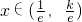 时,f(x)单调递减;
时,f(x)单调递减;
 时,f(x)单调递增
时,f(x)单调递增
故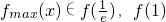 (8分)
(8分)
又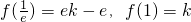
当ek-e>k,即 时,
时,

当ek-e≤k,即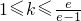 时,
时,
fmax(x)=f(1)=k(10分)
(III)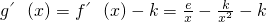 ,
,
∵g(x)在 在是减函数,
在是减函数,
∴g'(x)≤0在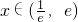 上恒成立
上恒成立
即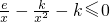 在
在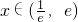 上恒成立,
上恒成立,
∴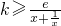 在
在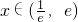 上恒成立,(12分)
上恒成立,(12分)
又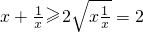 当且仅当x=1时等号成立.
当且仅当x=1时等号成立.
∴ ,∴
,∴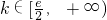 (14分)
(14分)
解法二;(I),(II)同解法一
(III)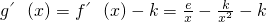 ,
,
∵g(x)在 是减函数,
是减函数,
∴g'(x)≤0在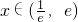 上恒成立
上恒成立
即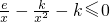 在
在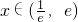 上恒成立
上恒成立
令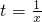 ,则
,则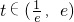 ,从而
,从而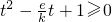 ,在
,在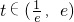 上恒成立.(12分)
上恒成立.(12分)
不妨设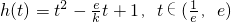
当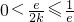 ,即
,即 时,有
时,有 ,
,
则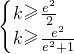 ,∴
,∴ .(14分)
.(14分)
分析:利用导数工具研究函数的极值,单调性与最值问题.
(1)x0是极值点导数值为0,函数值也为0,解方程得k.
(2)函数在闭区间上的最值:先利用导数判断单调性,后求最值.
(3)函数在区间上是减函数故其导数在该区间上≤0恒成立,故可解得k的范围.
点评:本题关键是要明确导数在函数的单调性,极值,最值中的应用.
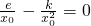 ,(2分)
,(2分)∴
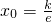 ,又f(x0)=0,即
,又f(x0)=0,即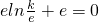 ,∴k=1.(4分)
,∴k=1.(4分)(II)
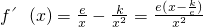 ,
,∵1≤k≤e,∴
 ,(6分)
,(6分)由此得
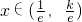 时,f(x)单调递减;
时,f(x)单调递减; 时,f(x)单调递增
时,f(x)单调递增故
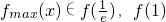 (8分)
(8分)又
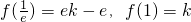
当ek-e>k,即
 时,
时,
当ek-e≤k,即
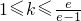 时,
时,fmax(x)=f(1)=k(10分)
(III)
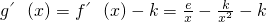 ,
,∵g(x)在
 在是减函数,
在是减函数,∴g'(x)≤0在
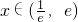 上恒成立
上恒成立即
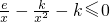 在
在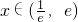 上恒成立,
上恒成立,∴
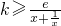 在
在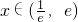 上恒成立,(12分)
上恒成立,(12分)又
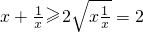 当且仅当x=1时等号成立.
当且仅当x=1时等号成立.∴
 ,∴
,∴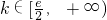 (14分)
(14分)解法二;(I),(II)同解法一
(III)
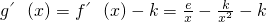 ,
,∵g(x)在
 是减函数,
是减函数,∴g'(x)≤0在
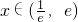 上恒成立
上恒成立即
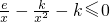 在
在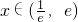 上恒成立
上恒成立令
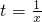 ,则
,则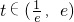 ,从而
,从而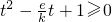 ,在
,在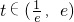 上恒成立.(12分)
上恒成立.(12分)不妨设
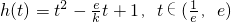
当
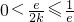 ,即
,即 时,有
时,有 ,
,则
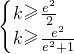 ,∴
,∴ .(14分)
.(14分)分析:利用导数工具研究函数的极值,单调性与最值问题.
(1)x0是极值点导数值为0,函数值也为0,解方程得k.
(2)函数在闭区间上的最值:先利用导数判断单调性,后求最值.
(3)函数在区间上是减函数故其导数在该区间上≤0恒成立,故可解得k的范围.
点评:本题关键是要明确导数在函数的单调性,极值,最值中的应用.

练习册系列答案
相关题目